1 梯度下降和 \(\beta\)

这是梯度下降的公式

\[J(\theta) = \frac{1}{2}\sum(y-\hat y_{\theta})^2\]

这里的\(y\)和\(x\)都是训练集给定的，如果要减小\(J(\theta)\)只能通过不断变动向量\(\theta\)的值，从而得到最小的\(J(\theta)\)。

2 三种梯度下降方式

• 批量梯度下降法BGD: 全量
• 随机梯度下降法SGD: 一个
• min-batch 小批量梯度下降法MBGD: 若干个

三者的区别在于梯度下降时\(J(\theta)\)使用样本的大小。、

\[\theta_j:= \theta_j 0- \alpha \frac{\partial}{\partial \theta_j}J(\theta)\]

这是每个\(\theta_j\)更新的方式。 这里以批量梯度下降法BGD的方式，进行推导。

\[\begin{alignat}{2} \frac{\partial}{\partial \theta_j}J(\theta) &= \frac{\partial}{\partial \theta_j}\frac{1}{2}(y-\hat y)^2 \\ &= \frac{1}{2} \cdot 2(y-\hat y) \cdot \frac{\partial}{\partial \theta_j}(y-\hat y) \\ &= (y-\hat y) \cdot \frac{\partial}{\partial \theta_j}(\sum(y_i-\theta x_i)) \\ &= (y-\hat y) \cdot (-x_i) \\ &= \frac{1}{m} \sum_{i=1}^m(y-\hat y) \cdot (-x_i) \\ \end{alignat}\]

• 批量梯度下降法BGD: 全量

\[\theta_j:= \theta_j + \frac{1}{m} \sum_{i=1}^m(y_i-\hat y) \cdot x_i\]

• 随机梯度下降法SGD: 一个

\[\theta_j:= \theta_j + (y_i-\hat y) \cdot x_i\]

• min-batch 小批量梯度下降法MBGD: 若干个

\[\theta_j:= \theta_j + \alpha \cdot \frac{1}{10} \sum_{i=1}^{i+9}(y_i-\hat y) \cdot x_i\] # 神经网络的bias的定义

bias其实就是每个方程的截距。

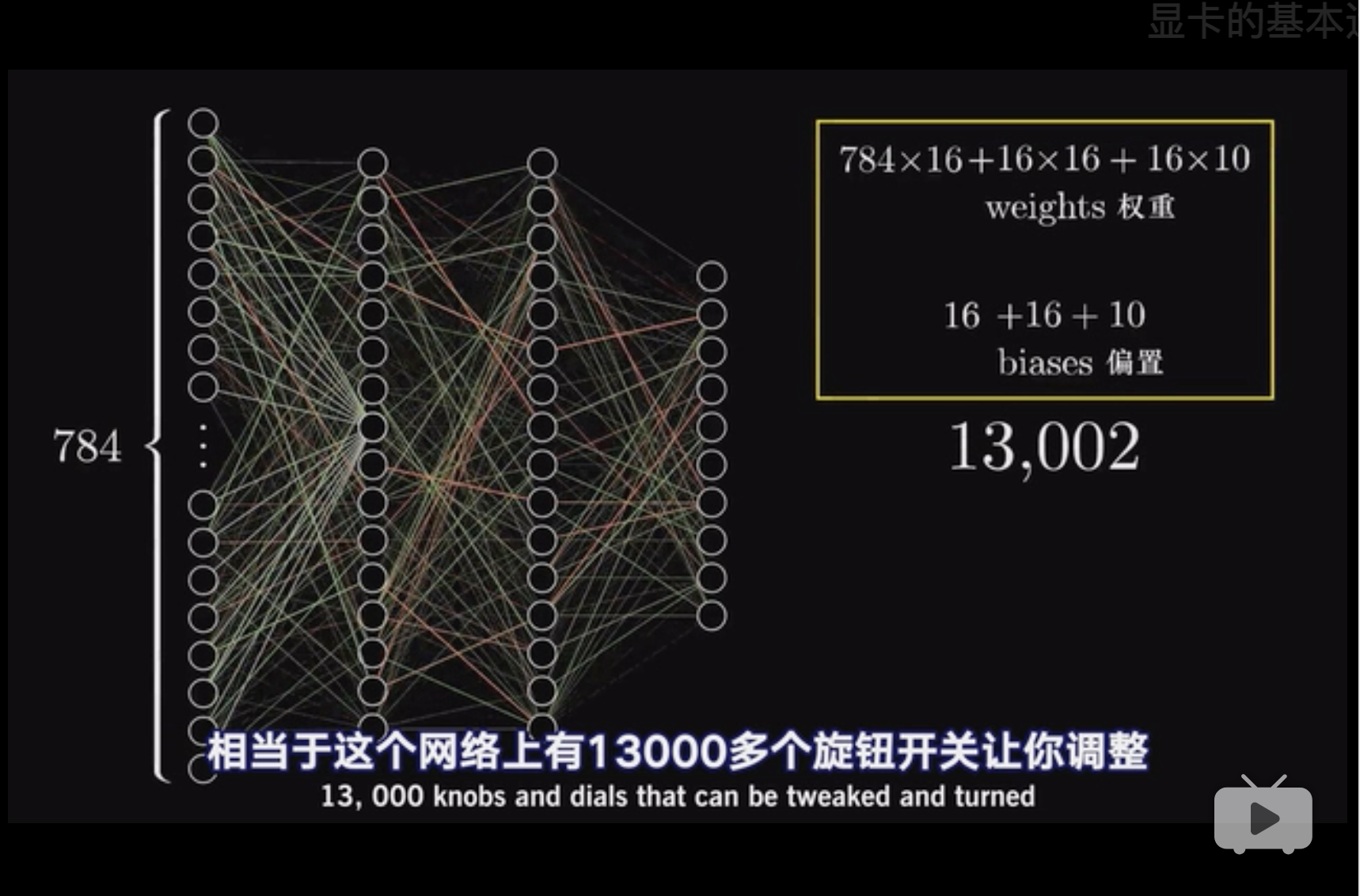
每个节点都有一个bias，一次一共有16个bias。 因此到目前为止，\(784 \times 16\)个\(w\)和\(16\)个bias。 (3Blue1Brown 2018a)

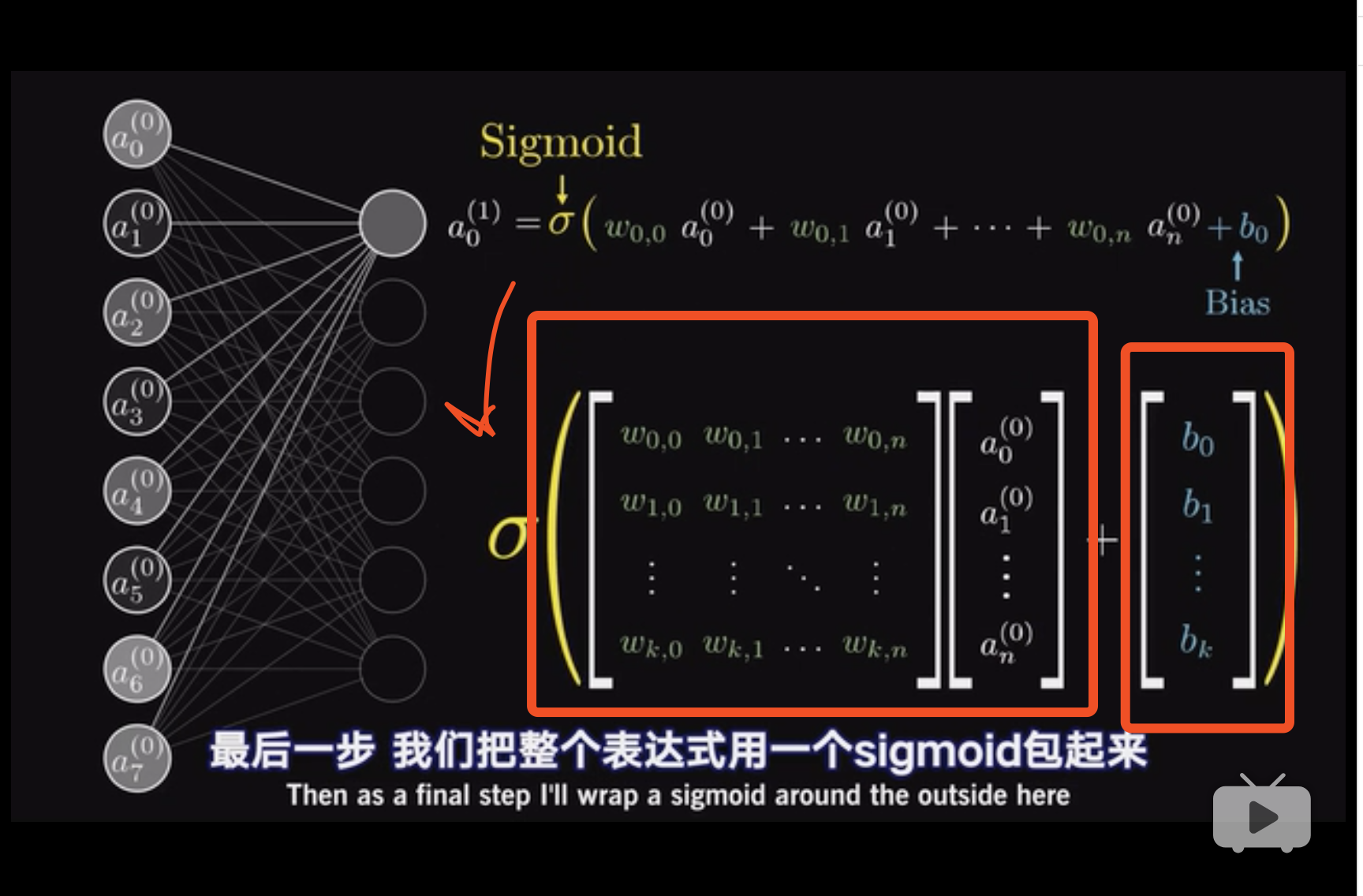
这是全部弄下来的bias数量和\(w\)数量。

于是转化成了线性代数的问题。 这个地方对线性代数的解释非常到位(14:26) 。

\[\alpha^{(1)} = \sigma(\mathcal W \alpha^{(0)} + b)\]

这里\(\alpha^{(i)}\)表示第几层。

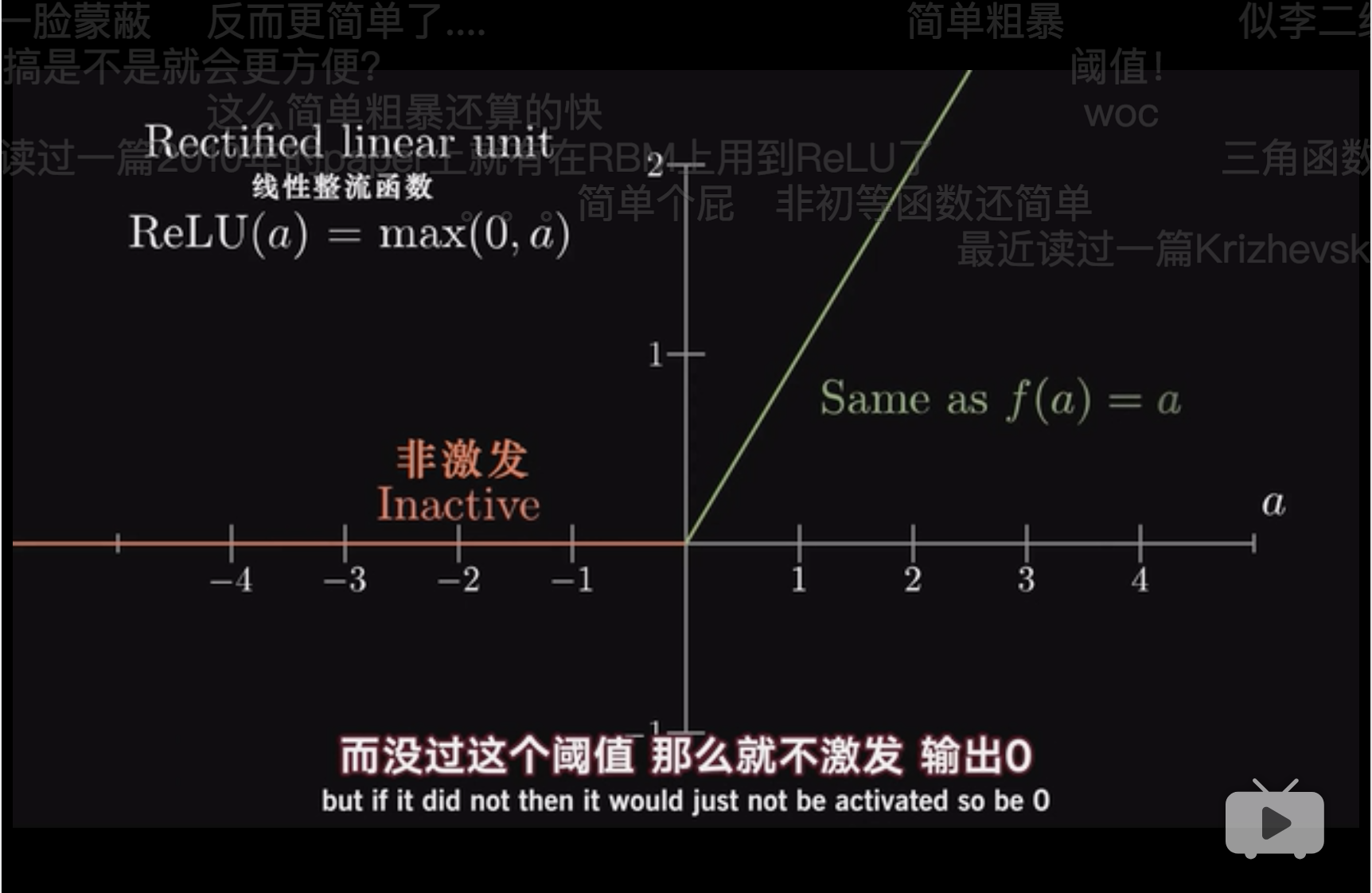
Relu其实一点都不简单，关键是为了描述突变，描述\(inactive \to active\)。

3 梯度下降一定是按照最陡的方向 (忆臻 2018)

假设，空间点从A点移动到B点。 空间两个特征变量\(x_1\)和\(x_2\)，\(z=f(x)\)是损失函数，\(x = [x_1,x_2]\)。 假设\(x\to x+\Delta x\)，\(\Delta x\)是移动的向量，那么，

\[\Delta z = f(x+\Delta x)-f(x)\]

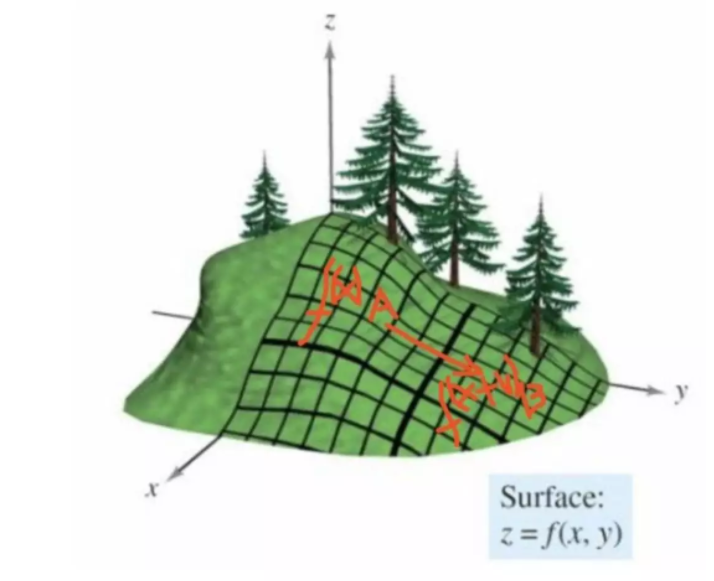
使用泰勒公式，近似得到，

\[\begin{alignat}{2} \Delta z & = f(x+\Delta x)-f(x) \\ & = \nabla f^T(x) \Delta x \end{alignat}\]

\(\nabla f^T(x)\)是各种偏导集合的矩阵¹。不理解的话，就当成一阶导数理解吧。 并且这句是梯度下降公式中的梯度。 注意这里\(\nabla f^T(x)\)和\(\Delta x\)是两个向量，\(\nabla f^T(x)\)显然是x点的切线方向， \(\Delta x\)是移动向量方向。

要下降最快，就是说， \[\begin{alignat}{2} \max \Delta z & \to \max \nabla f^T(x) \Delta x \\ & \to \max ||\nabla f^T(x)||\cdot ||\Delta x|| \cos(\theta) \\ & \to \max \cos(\theta) \\ & \to \theta = 0 \end{alignat}\]

因此当移动方向是切线方向是下降最快的。

4 神经网络的过程 (3Blue1Brown 2018b)

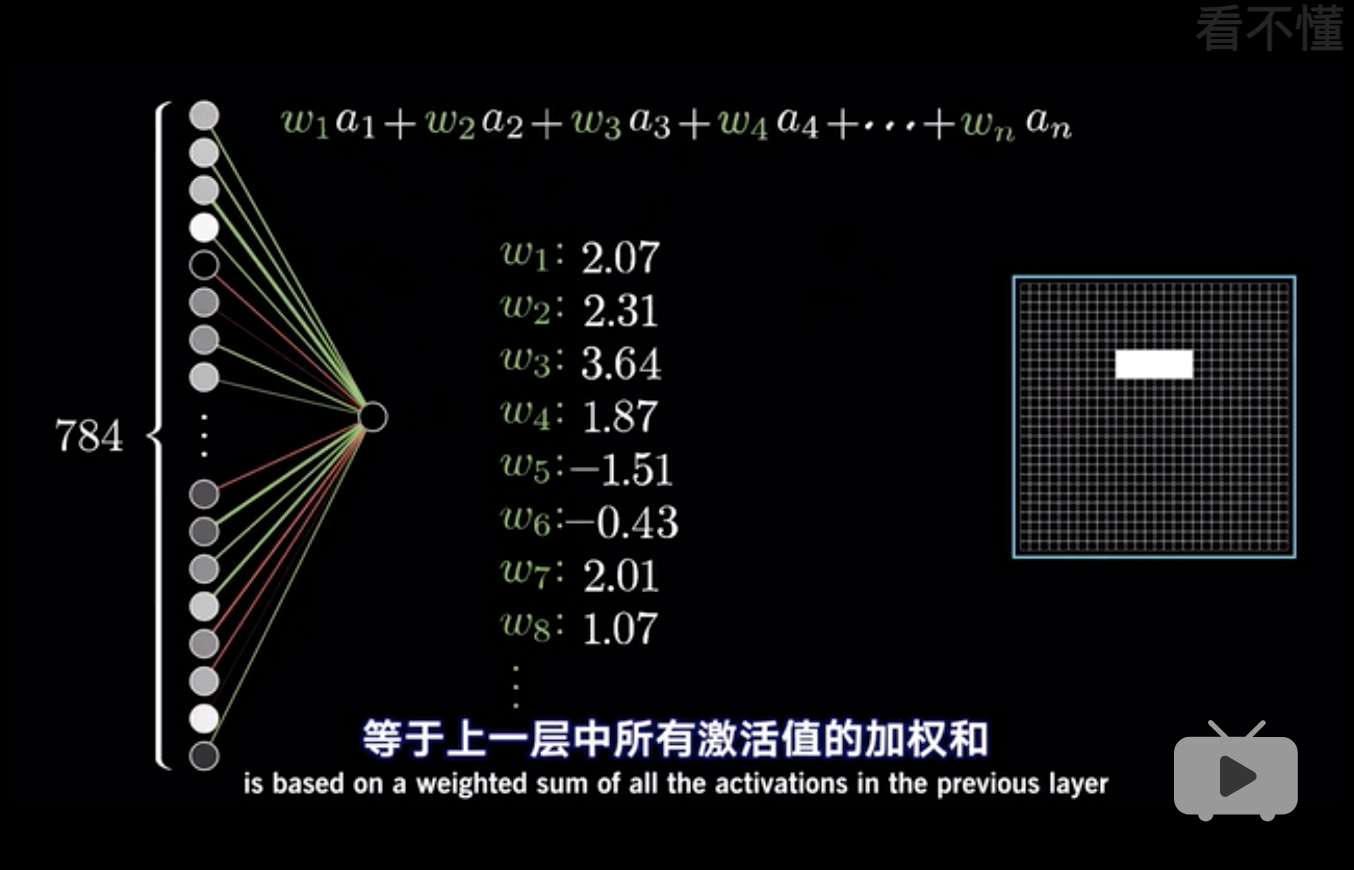
无隐藏层的神经网络就是一般线性方程。

最形象的图， 输入层784个节点， 第一层隐藏层16个，相当于每个输入层的节点都跟第一层隐藏层的节点链接。 第二个隐藏层16个， 输出层10个。 因此\(w\)有\(784 \times 16 + 16 \times 16 + 16 \times 10\)。

定义好后，梯度下降，找最合适的\(\theta\)，使得损失最小。

这里有13000个\(w\)，但是都是一个列向量而已，用 \(\nabla C(W) = \frac{\partial C}{\partial w}\)表示。 13000个分力最后会给出一个合力。

最后这张图解释了，虽然在点\((1,1)\)但是明显最快方向为\((3,1)\)也就是说，梯度下降不一定是直线的，会拐弯。 因此梯度下降一定是按照最陡的方向(3)。