很老的笔记，总结一下。

供需求函数

${\begin{cases} q_{t}^{D} & = α_{0} + α_{1} p_{t} + u_{t} \\ q_{t}^{S} & = β_{0} + β_{1} p_{t} + v_{t} \\ q_{t}^{D} & = q_{t}^{S} \end{cases}$

这是供需求函数，我们肯定不能直接用 $q_{t} = α_{0} + α_{1} p_{t} + u_{t}$ 去跑回归。因为我们首先不知道这是代表供给还是需求函数，实际上谁也不是。

${\begin{cases} q_{t} & = α_{0} + α_{1} p_{t} + u_{t} \\ q_{t} & = β_{0} + β_{1} p_{t} + v_{t} \end{cases}$

解得：

$\begin{aligned} p_{t} & = \frac{β_{0} - α_{0}}{β_{1} - α_{1}} + \frac{v_{t} - u_{t}}{β_{1} - α_{1}} \\ p_{t} & \sim v_{t}, u_{t} \end{aligned}$

我们知道，当 $x$ 和 $μ$ 线性相关， $x$ 就是内生了(陈强 2014)。

这个时候我们需要引入 工具变量，假设是天气 $x_{t}$ 。

工具变量的两个条件：

在供给方程中，天气影响 $p_{t}$ 的，因此 $C o v (p_{t}, x_{t}) \neq 0$ ¹。
$x_{t}$ 和 $u_{t}, v_{t}$ 都不像相关，天气是外生的，除了自身，不受到其他变量决定。

重新写供给函数

${\begin{cases} q_{t}^{S} & = β_{0} + β_{1} p_{t} + β x_{t} + v_{t} \\ q_{t}^{S} & = β_{0} + β_{1} p_{t} \overset{ρ > 0}{\leftarrow} β x_{t} \overset{\times}{\to} v_{t} \end{cases}$

所以，

这里涉及到 2SLS

第一步，

$\begin{aligned} p_{t} & = γ_{0} + γ_{1} x_{t} + δ_{t} \\ p_{t} & = \hat{p_{t}} (x_{t}) + {\hat{δ}}_{t} \end{aligned}$

第二步，

${\begin{cases} q_{t} & = α_{0} + α_{1} \hat{p_{t}} + u_{t} + α_{1} (p_{t} - \hat{p_{t}}) \\ q_{t} & = β_{0} + β_{1} \hat{p_{t}} + v_{t} + β_{1} (p_{t} - \hat{p_{t}}) \end{cases}$

${\begin{cases} q_{t} & = α_{0} + α_{1} ({\hat{γ}}_{0} + {\hat{γ}}_{1} x_{t}) + u_{t} + α_{1} (p_{t} - \hat{p_{t}}) \\ q_{t} & = β_{0} + β_{1} ({\hat{γ}}_{0} + {\hat{γ}}_{1} x_{t}) + v_{t} + β_{1} (p_{t} - \hat{p_{t}}) \end{cases}$

然后就可以回归了。

矩估计

一矩： $E (x) = μ$
二矩： $E (x^{2}) = V a r (x) + E^{2} (x) = σ^{2} + μ^{2}$

如果我们假设 $x \sim N (μ, σ)$ ，有两个未知数，因此我们需要两个假设， $μ$ 和 $σ$ ，并使用两个方程去估计，就是我们的矩。通常我们用样本矩来猜测，

${\begin{cases} \frac{1}{n} \sum_{i = 1}^{n} x_{i} = \hat{μ} \\ \frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} = {\hat{μ}}^{2} + {\hat{σ}}^{2} \end{cases}$

因此任意的 $f (x)$ 都可以叫做矩估计。

这里我们使用第二个假设，

$\begin{aligned} E (z_{i} ϵ_{i}) & = 0 \\ E (z_{i} (y_{i} - x_{i}^{^{'}} β)) & = 0 \\ E (z_{i} y_{i}) & = E (z_{i} x_{i}^{^{'}}) \cdot β \\ E (z_{i} x_{i}^{^{'}})^{- 1} E (z_{i} y_{i}) & = β \end{aligned}$

我们用样本估计，来估计总体估计！！！

$\begin{aligned} E (z_{i} x_{i}^{^{'}})^{- 1} E (z_{i} y_{i}) & = β \\ \hat{β} & = (\frac{1}{n} \sum_{i = 1}^{n} z_{i} x_{i}^{^{'}})^{- 1} (\frac{1}{n} \sum_{i = 1}^{n} z_{i} y_{i}) \\ \hat{β} & = (z_{i} x_{i}^{^{'}})^{- 1} (z_{i} y_{i}) \end{aligned}$

样本矩除了 $E (β)$ ，还有 $V a r (β)$ 要估计。

$\begin{aligned} \hat{β} - β & = (z_{i} x_{i}^{^{'}})^{- 1} z_{i} (x^{^{'}} β + ϵ) - β \\ \hat{β} - β & = (z_{i} x_{i}^{^{'}})^{- 1} z_{i} x^{^{'}} β + (z_{i} x_{i}^{^{'}})^{- 1} z_{i} ϵ - β \\ \hat{β} - β & = β + (z_{i} x_{i}^{^{'}})^{- 1} z_{i} ϵ - β \\ \hat{β} - β & = (z_{i} x_{i}^{^{'}})^{- 1} z_{i} ϵ \\ \hat{β} - β & = (\frac{1}{n} \sum_{i = 1}^{n} z_{i} x_{i}^{^{'}})^{- 1} (\frac{1}{n} \sum_{i = 1}^{n} z_{i} ϵ_{i}) \\ \hat{β} - β & = S_{Z X}^{- 1} \bar{g} \end{aligned}$

这里假设 $S_{Z X}^{- 1} = (\frac{1}{n} \sum_{i = 1}^{n} z_{i} x_{i}^{^{'}})^{- 1}$ 、 $\bar{g} = (\frac{1}{n} \sum_{i = 1}^{n} z_{i} ϵ_{i})$ 。

因此用样本估计估计总体估计时，我们假设在大样本的情况下，

$S_{Z X}^{- 1} \bar{g} \overset{大样本}{\to} E (S_{Z X}^{- 1} \bar{g}) = E (S_{Z X}^{- 1}) E (\bar{g}) = E (S_{Z X}^{- 1}) \cdot 0 = 0$

注意这里 $E (S_{Z X}^{- 1})$ 是一个数，所以可以分离。

所以 $E (\hat{β} - β) = 0 \to E (\hat{β}) = β$

$\begin{aligned} A v a r (\hat{β}) & = E ((\hat{β} - β)^{2}) \\ = E ((S_{Z X}^{- 1} \bar{g})^{2}) \\ \dots \end{aligned}$

这里有比较简单的推导方法。

第一个方程是 $\begin{aligned} x & \sim z \\ \hat{γ} & = (z^{^{'}} z)^{- 1} z^{^{'}} x \\ \hat{x} & = z \hat{γ} \\ = z [(z^{^{'}} z)^{- 1} z^{^{'}} x] \\ = [z (z^{^{'}} z)^{- 1} z^{^{'}}] x & = p x \end{aligned}$

同理 $\begin{aligned} \hat{β} & = (\hat{x} \hat{x})^{- 1} \hat{x} y \\ \hat{β} & = (x^{^{'}} P^{^{'}} P x)^{- 1} \hat{x} y \\ \hat{β} & = (x^{^{'}} P x)^{- 1} \hat{x} y \\ \hat{β} & = (x^{^{'}} \hat{x})^{- 1} \hat{x} y \\ \hat{β} & = (z x)^{- 1} z y \end{aligned}$

full rank 就是矩估计的条件

能够作为工具变量的变量数量不能少于内生变量的数量。

弱工具变量检验

Shea’s partial $R^{2}$

假设 $y = x_{1}^{^{'}} β_{1} + x_{2} β_{2} + μ$ ，其中只有 $x_{2}$ 是内生的，工具变量为 $z_{2}$ 。做回归 $x_{2} \sim x_{1}^{^{'}} \to e_{1}$ 和 $z_{2} \sim x_{1}^{^{'}} \to e_{2}$ 。其中 $e_{1}$ 和 $e_{2}$ 分别衡量了 $x_{2}$ 和 $z_{2}$ 除了 $x_{1}^{^{'}}$ 以外的其他波动。再做 $e_{1} \sim e_{2} \to R_{p}^{2}$ ，如果 $R_{p}^{2}$ 大，说明不是弱工具变量。

过度识别检验

$z$ 的数量超过内生的 $x$ 数量。只有这样 $E (z ϵ) = 0$ ，否则不满足因此，我们假设有K个 $x$ ，r个是内生的， $z$ 有 m个，因此回归，

$ϵ \sim x_{1} + \dots + x_{K - r} + z_{1} + \dots z_{m} + e r r o r$ 如果得到的 $R^{2}$ 大，或者说 $n R^{2}$ 比较于 $Θ^{2} (m - r)$ 而大的话，那么 $E (z ϵ) = 0$ 的条件就不满足了。因此要求 $R^{2}$ 尽可能低，即P值要小。

GMM

GMM是过度识别的时候使用，因为 $n (x) < n (z)$ 。这个时候 $\frac{1}{n} \sum_{i = 1}^{n} z_{i} (y_{i} - x^{^{'}} \hat{β})$ 不能等于0了，无解，但是可以使其平方最小。

一步还是两步

一步是满足同方差假设的，所以还是用两步吧。

弱工具变量容易有偏

$y = 1 + 2 x + μ$

强工具变量

$x = 0.5 z + 0.2 μ + 0.1 v$

弱工具变量

$x = 0.01 z + 0.2 μ + 0.1 v$

library(tidyverse)
beta_cb1 <- 1:100
beta_cb2 <- 1:100
a <- data_frame(
  mu = rnorm(100),
  v  = rnorm(100),
  z  = rnorm(100)
)

## Warning: `data_frame()` is deprecated as of tibble 1.1.0.
## Please use `tibble()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.

for (i in 1:100){
  
b <- 
  as.data.frame(resample_bootstrap(a)) %>% 
  mutate(
    x1 = 0.5*z + 0.2*mu + 0.1*v,
    x2 = 0.01*z + 0.2*mu + 0.1*v,
    y1 = 1 + 2*x1 + mu,
    y2 = 1 + 2*x2 + mu
  ) %>% 
  summarise(
    beta1 = sum(z*y1)/sum(z*x1),
    beta2 = sum(z*y2)/sum(z*x2)
  )
beta_cb1[i] <- b[1,1]
beta_cb2[i] <- b[1,2]
}
data_frame(
  beta1 = beta_cb1 %>% unlist(),
  beta2 = beta_cb2 %>% unlist()
) %>% 
  gather() %>% 
  ggplot(aes(x = value, y = ..density..,col = key)) + 
    geom_freqpoly() +
    labs(
      x = "预测的beta值，真实为2",
      y = "频率",
      subtitle = "弱工具变量在小样本下很容易不对称，有偏",
      title = "弱工具变量比较"
    ) +
  theme_minimal() +
  theme(text = element_text(family = "STKaiti"))

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

## Warning in grid.Call(C_stringMetric, as.graphicsAnnot(x$label)): Windows字体数据
## 库里没有这样的字体系列

## Warning in grid.Call(C_stringMetric, as.graphicsAnnot(x$label)): Windows字体数据
## 库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_stringMetric, as.graphicsAnnot(x$label)): Windows字体数据
## 库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call.graphics(C_text, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列

## Warning in grid.Call(C_textBounds, as.graphicsAnnot(x$label), x$x, x$y, :
## Windows字体数据库里没有这样的字体系列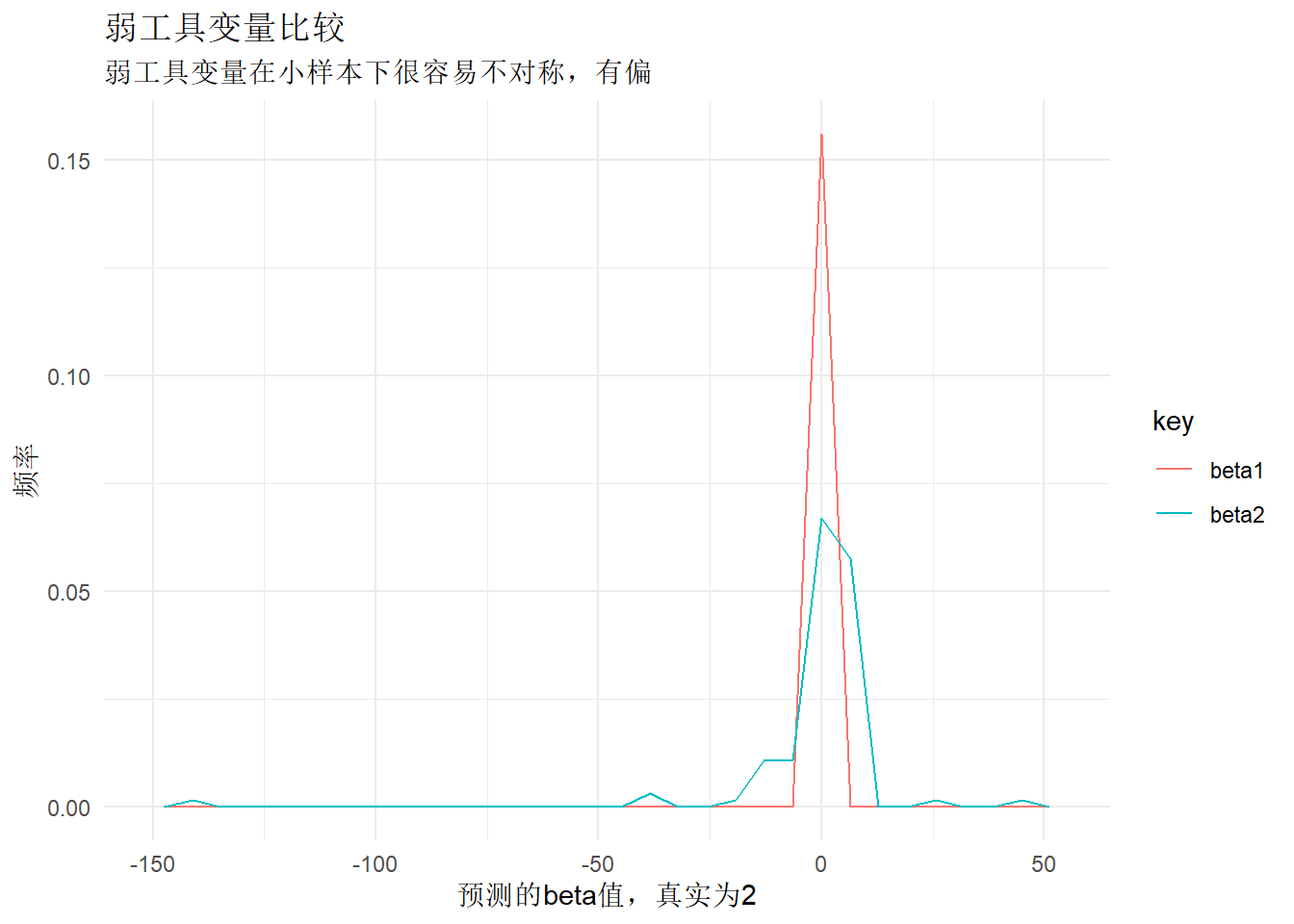

陈强. 2014. 高级计量经济学及Stata应用.第2版. 高等教育出版社.

这里的Cov，latex打印不出来。↩

GMM模型理解