1 决策树解决回归

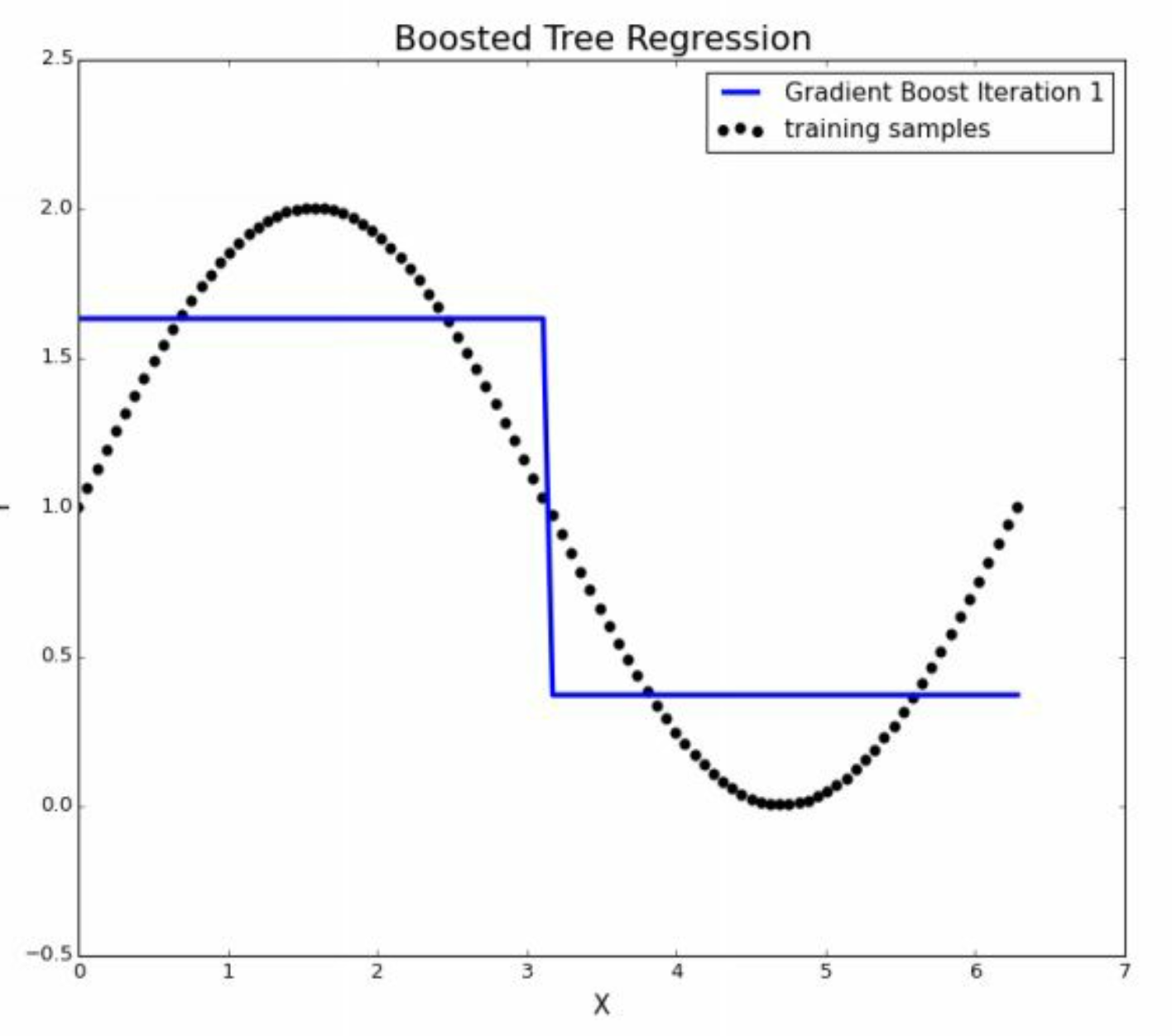
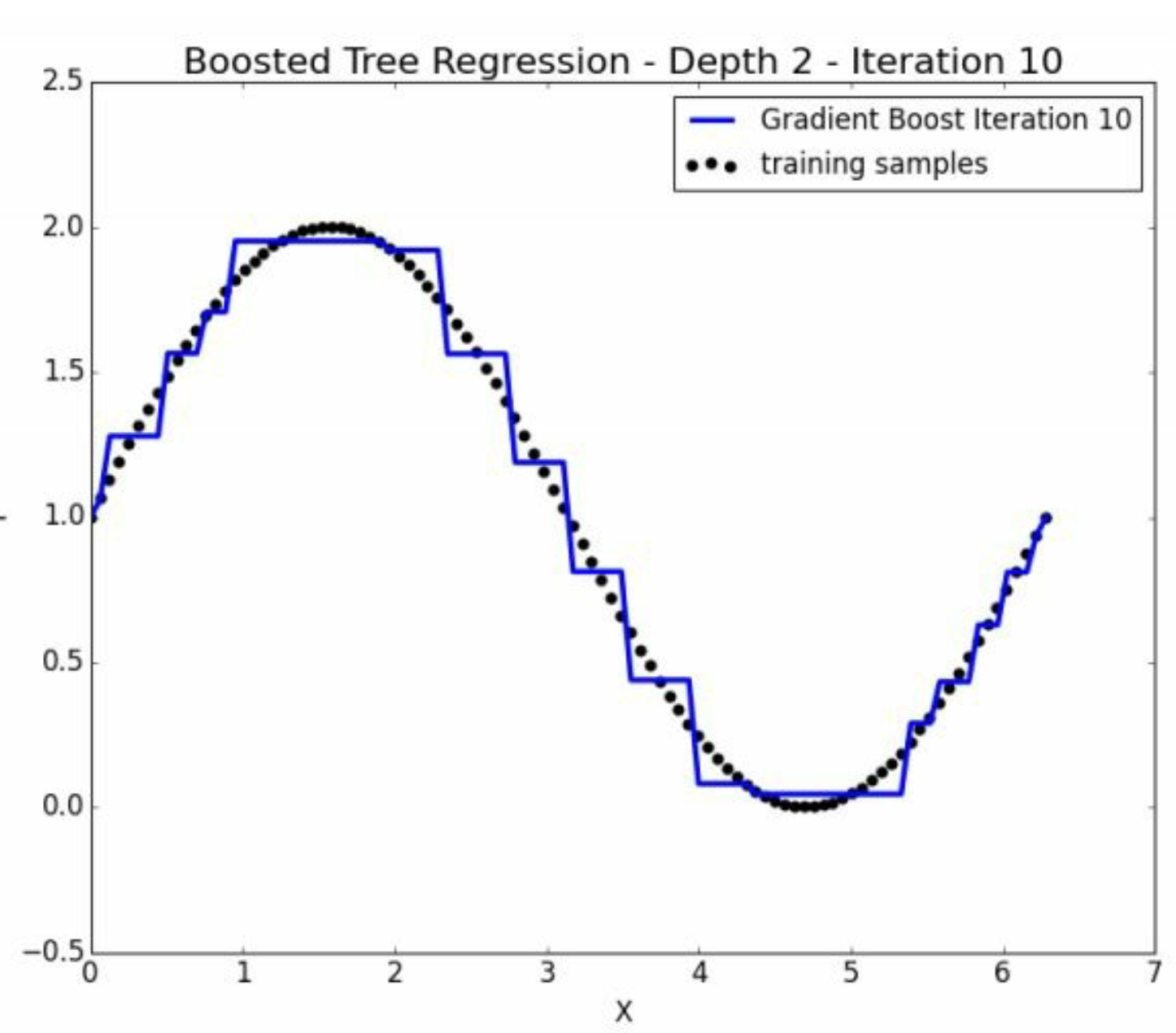
注意这两幅图，就是通过 $x$ 不断的切bin去完成对 $y$ 一个连续变量的预测，我们会发现，当 $x$ 进行不断切分的时候，也就是复杂程度增加的时候，冒着过拟合的风险，逐渐拟合了 非线性 的关系。因此也印证了，决策树预测非线性关系本身比较好。

2 决策树解决分类

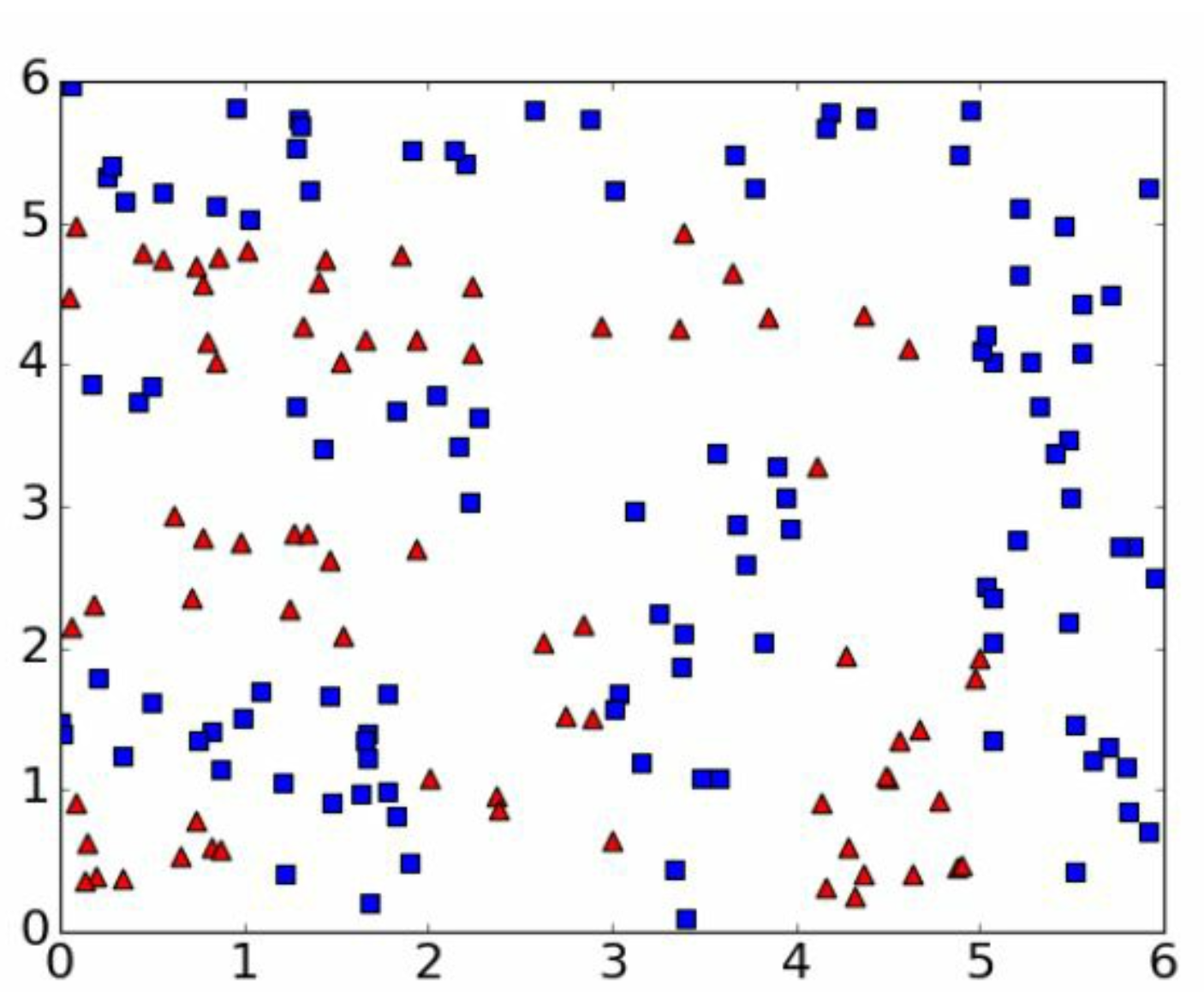
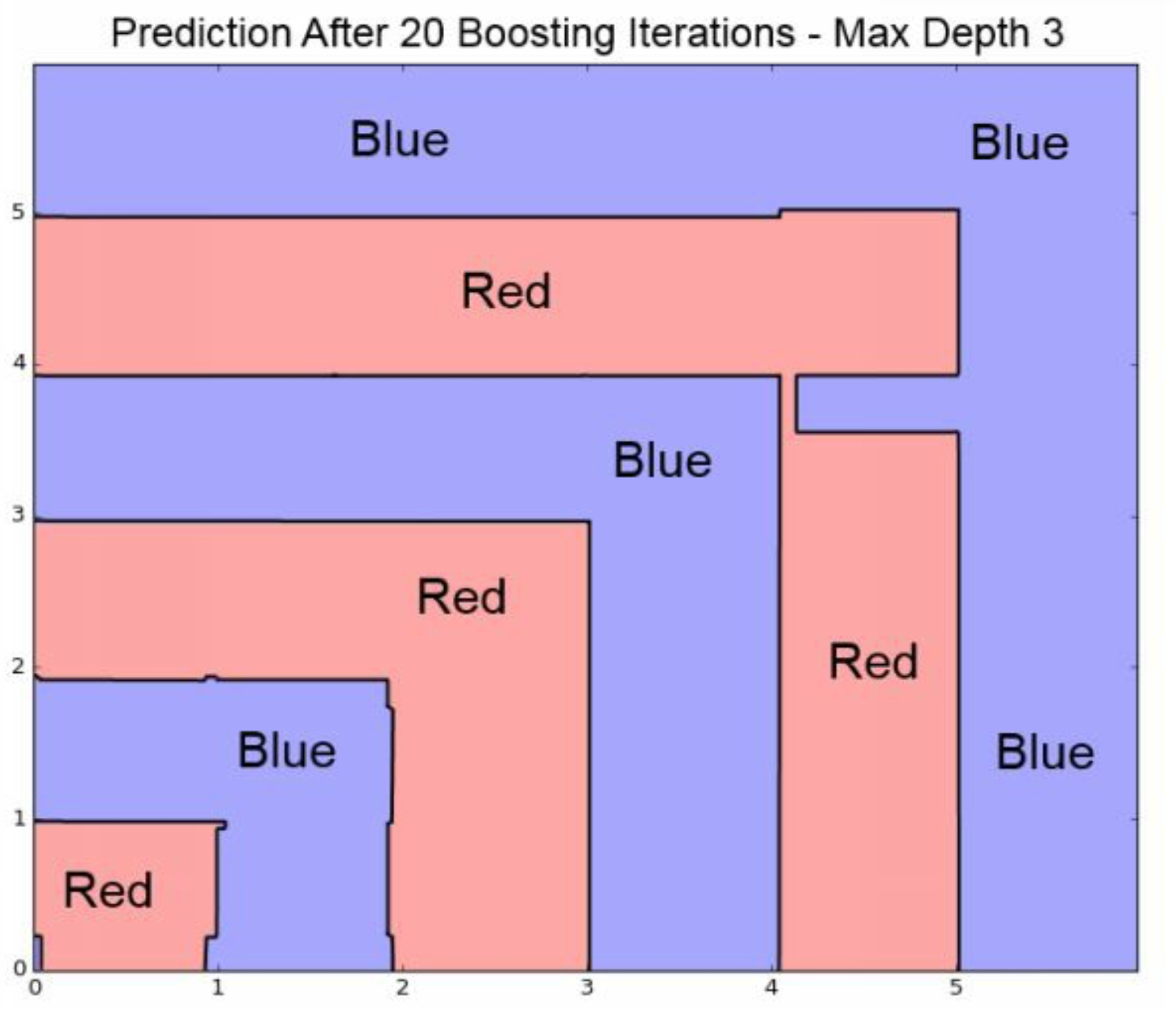
注意这幅图，这就是决策树对分类分类处理的逻辑，我们认为图中两个 $x$ ，连续的，然后一个 $y$ ，用有限的颜色标记。

3 Boosting的直觉

那么在树形结构上，决策树是一个if-then结构，那么boosting就是把决策树串联／并联起来。

4 weak learner的定义

对于一个分类，可能一个weak learner对 某些样本可以精准分类 ，某些不能。但是只要它擅长某一部分，或者只要比均匀分布瞎猜的好，我们就认为是weak learner。一群weak learner，分工处理自己擅长的地方，按照串联链接，那么就是boosting。因此串联的时候，好像按照时间进行的，不同的weak learner在正确的时间进行划分就好。如果按照bagging的思想，让他们同时做，然后求平均，实际上可能是十个weak的结果，得到1个weakly combined 产品。

不是特别听的懂，boosting连接的时候。 p.23 好无聊，还不如看pandas呢。

现在开始总结regression using boosting。

5 regression using boosting理解

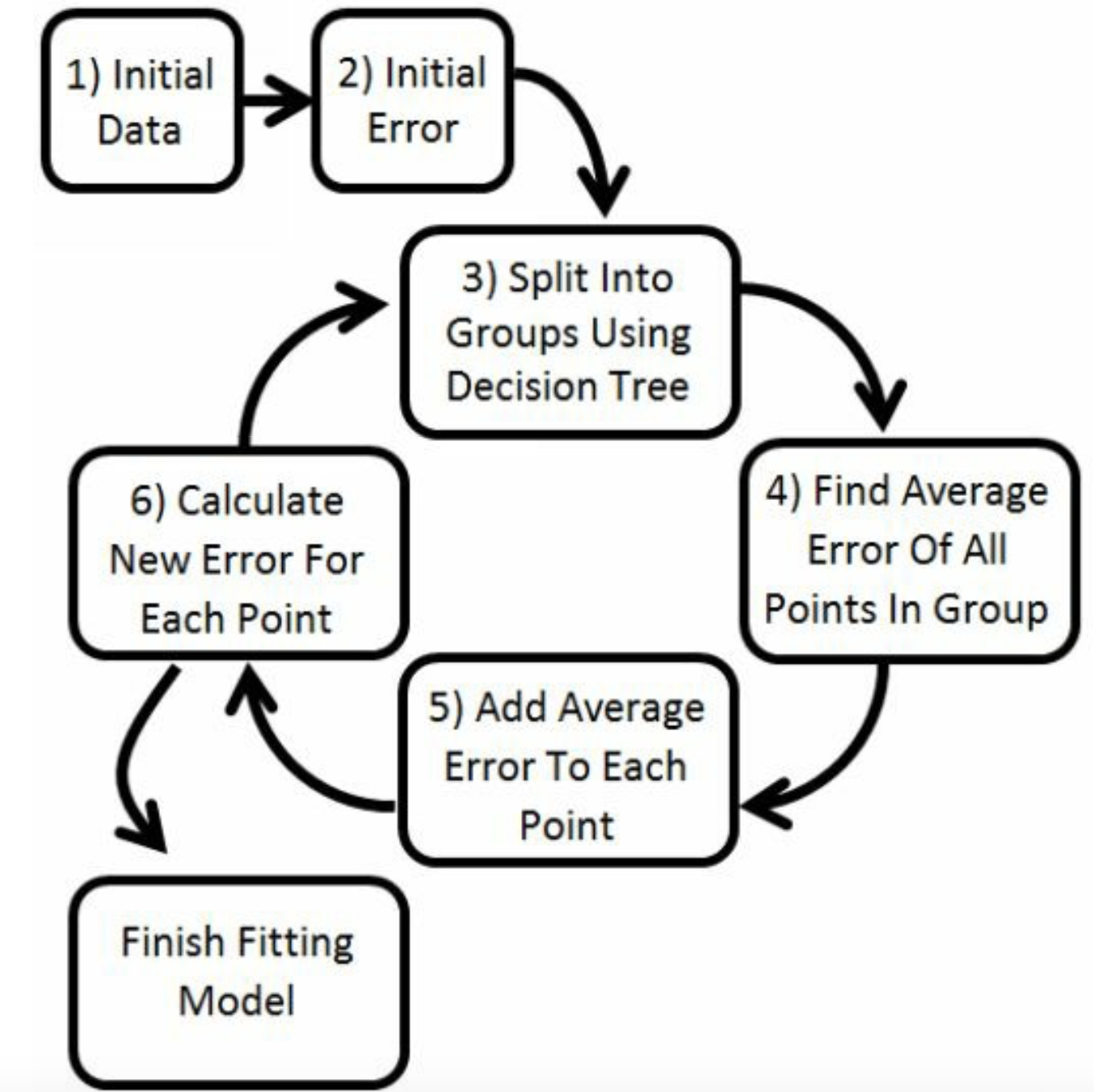
假设总体方程为

$Y = \sin x + 1$

显然就是把正弦函数上移一个单位。

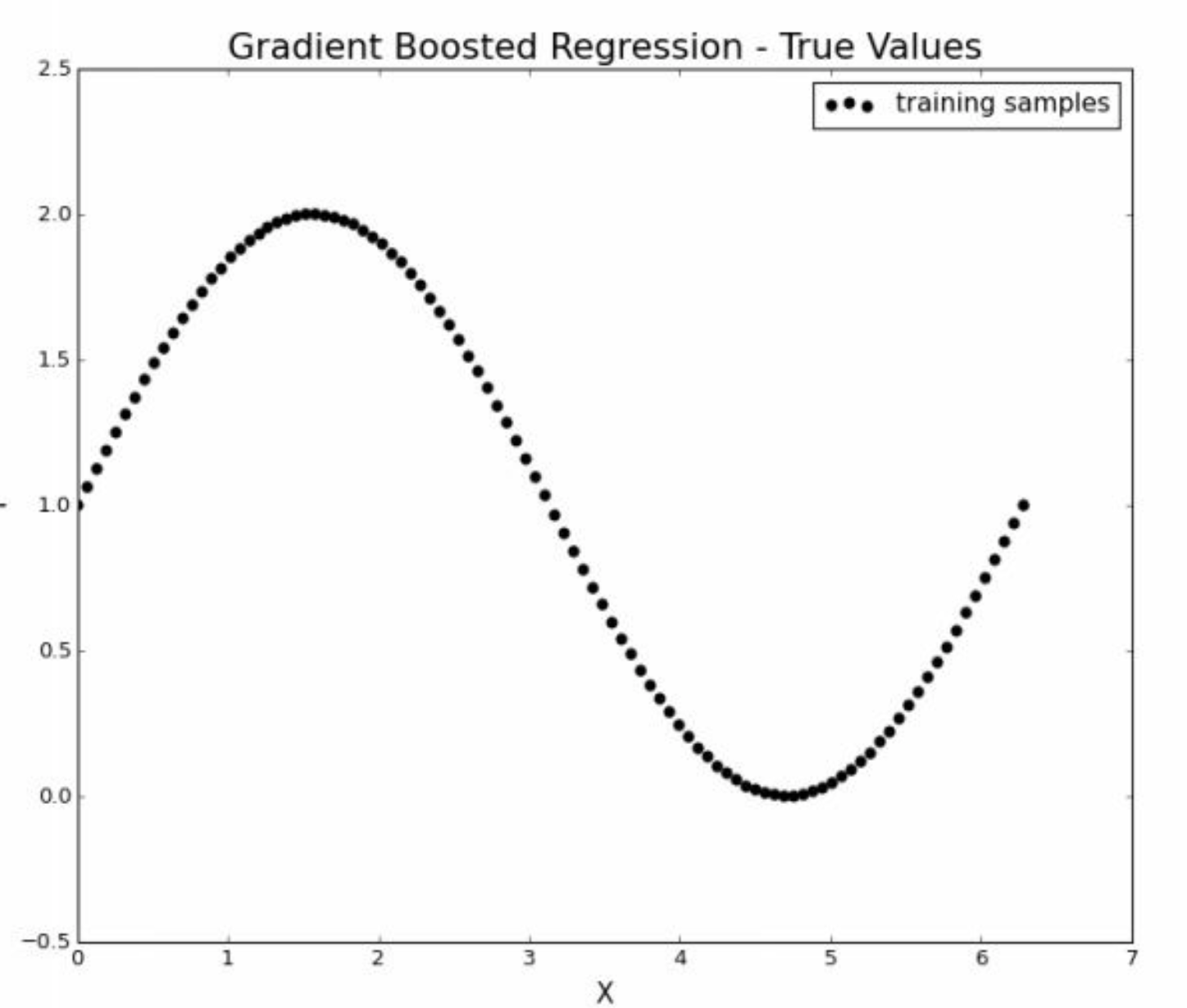
5.1 round=1

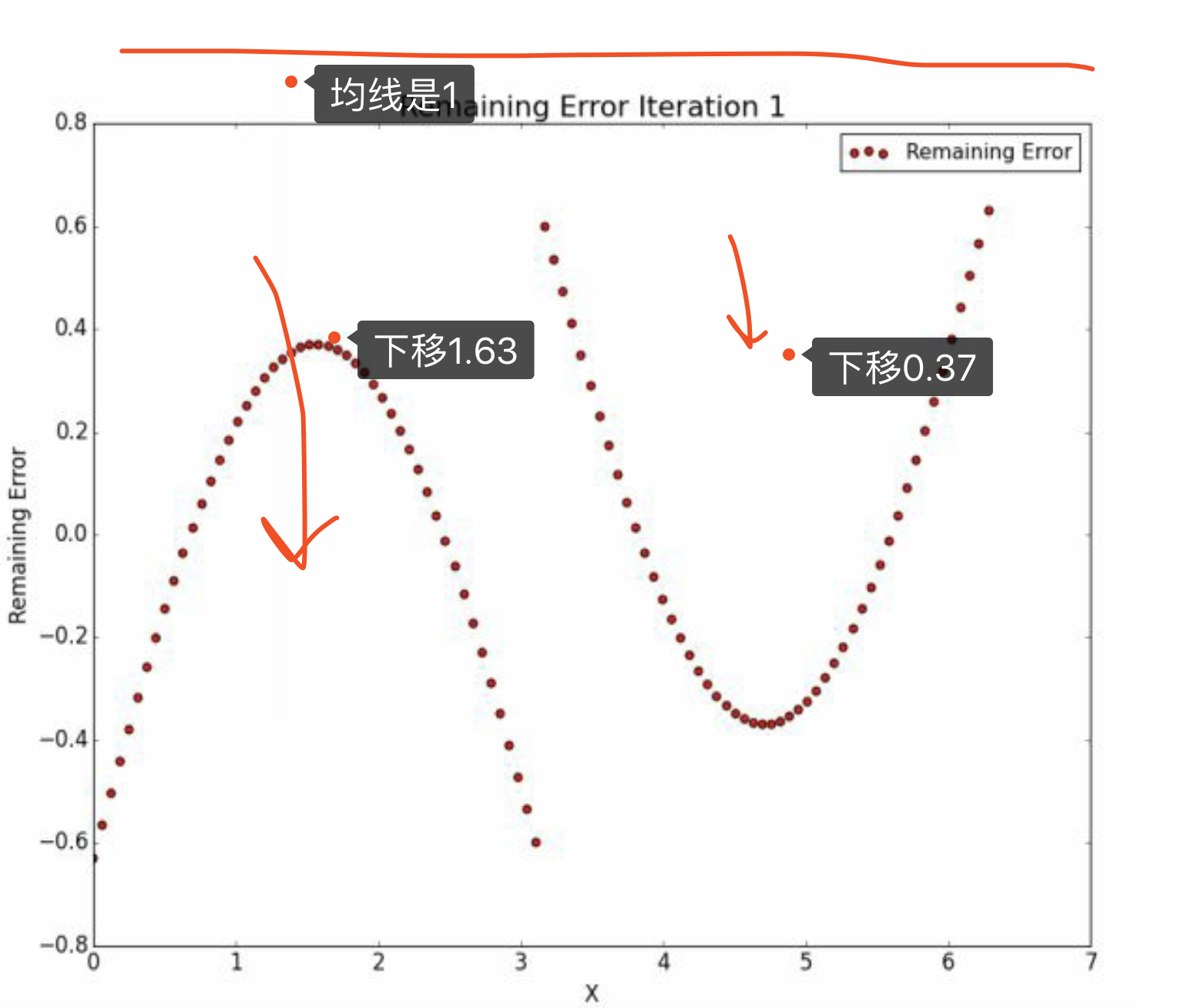
假设 ${\hat{y}}_{0} = 0$ 所以 $\hat{u} = y - \hat{y} = y$ 。然后我们取 $x$ 的中间值 $x = 3.14$ 进行决策树的第一个切割。注意这个时候， $\hat{u}$ 的变化曲线就是 $y$ 的变化曲线，所以我们不需要再画了。

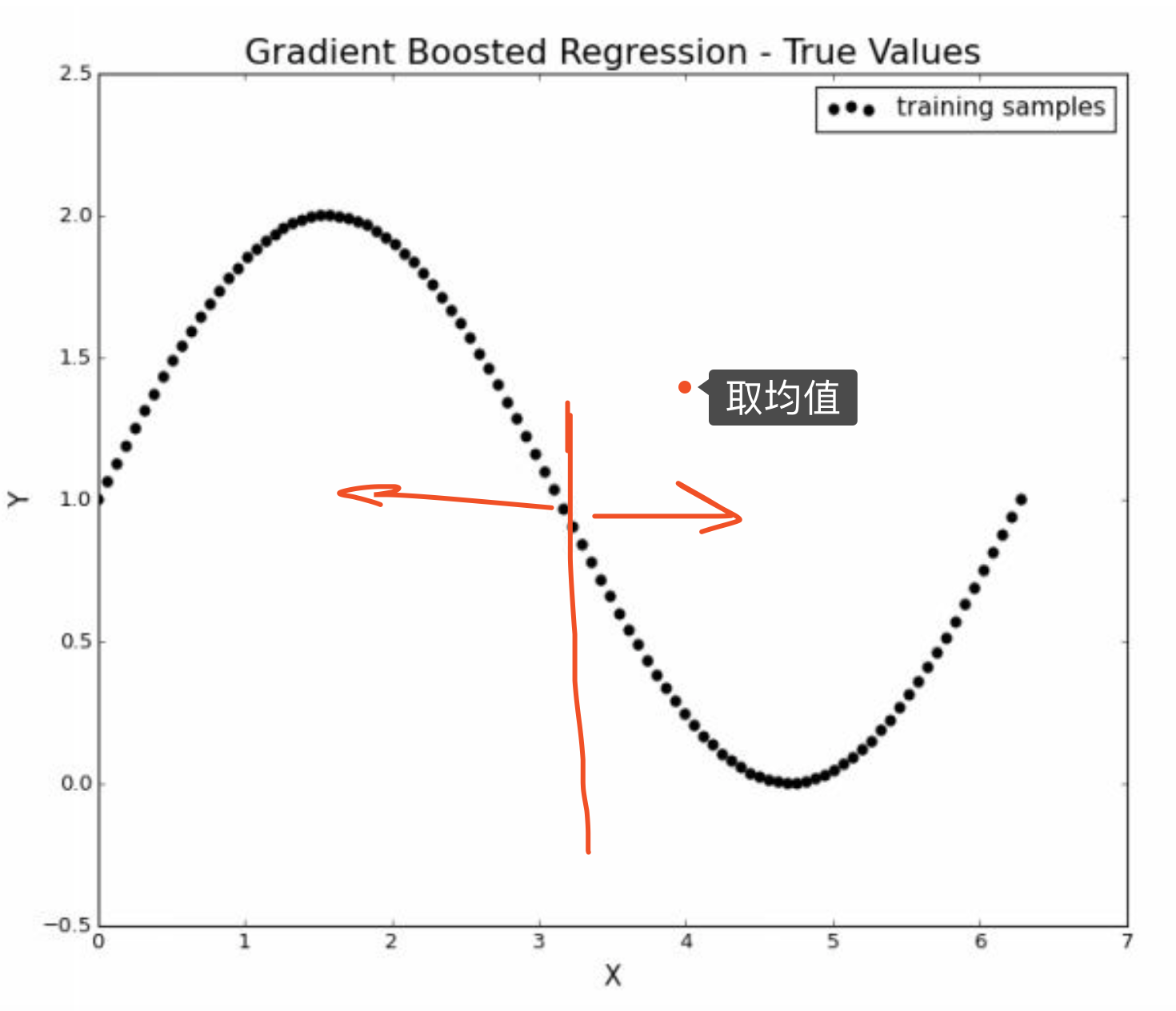
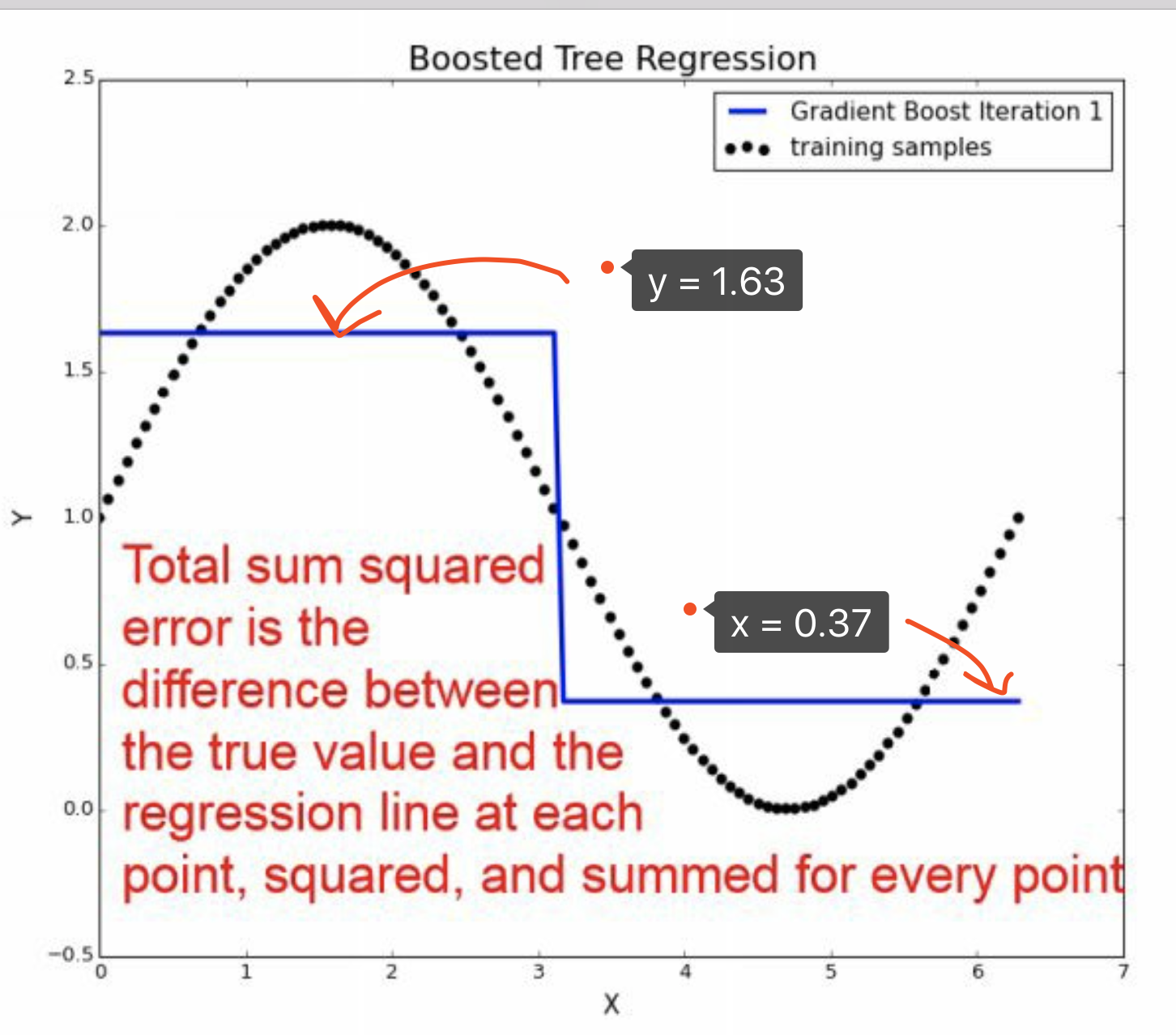
我们在各自的分样本中找到了均值，

${\hat{y}}_{2}^{(1)} = 1.63$

${\hat{y}}_{2}^{(2)} = 0.37$

$\begin{aligned} {\hat{u}}_{2} | 3.14 & = ({\hat{u}}_{1} | x < 3.14) - 1.63 \\ = 图像下移 \end{aligned}$

$\begin{aligned} {\hat{u}}_{2} | 3.14 & = ({\hat{u}}_{1} | x \geq 3.14) - 0.37 \\ = 图像下移，但是相对少 \end{aligned}$

5.2 round=2

通过第一次的boosting，我们的结果不是很好。那么我们可以开始第二次的boosting。

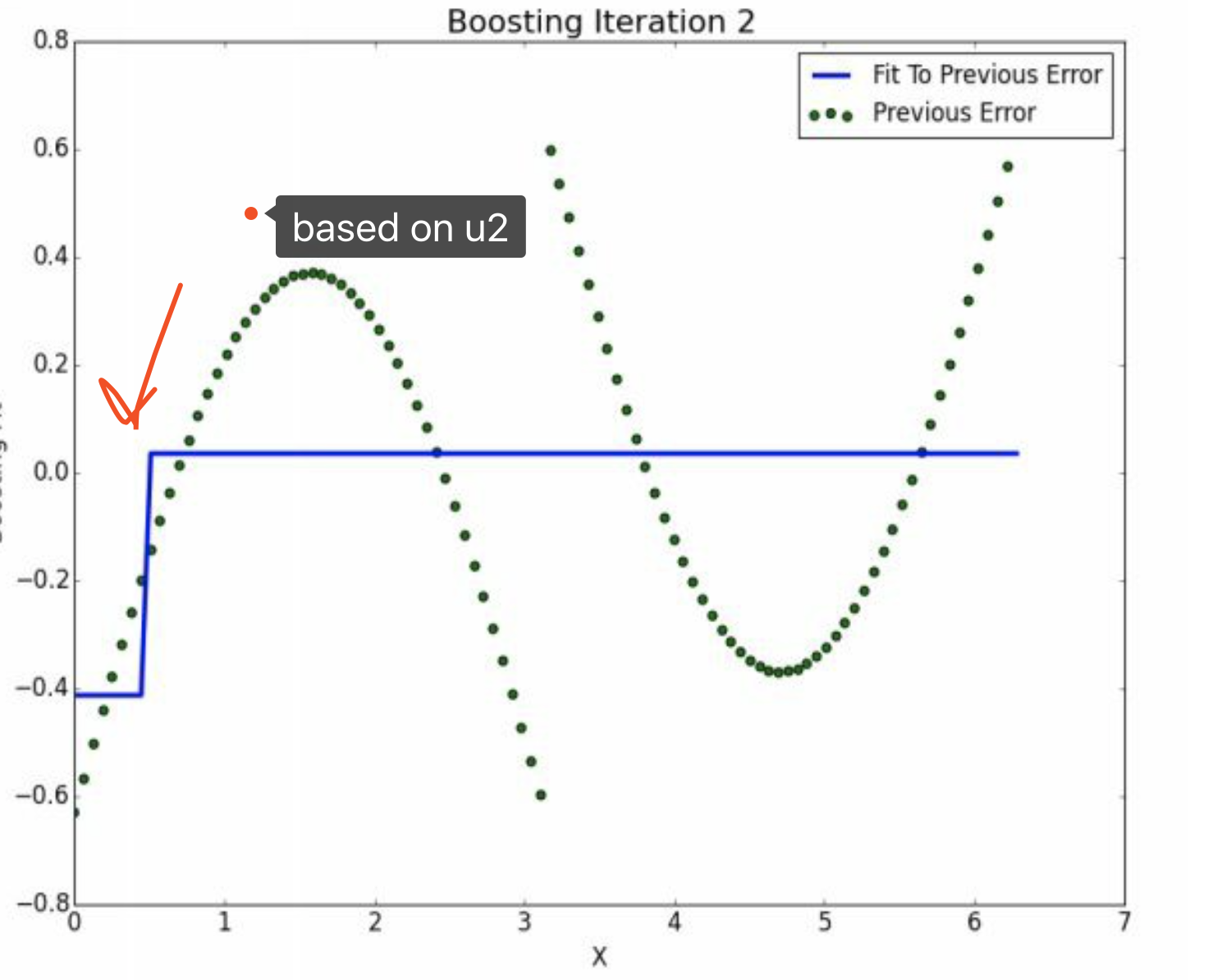
在原来 ${\hat{u}}_{2}$ 的基础是，我们再进行一次决策树¹。

横线衡量了分样本均值，公式可以这么书写。

$\begin{aligned} {\hat{u}}_{3} | x < 0.48 & = ({\hat{u}}_{2} | x < 0.48) - 0.40 \\ = 图像上移 \end{aligned}$

$\begin{aligned} {\hat{u}}_{3} | x < 0.48 & = ({\hat{u}}_{2} | x \geq 0.48) - 0.05 \\ = 图像下移，但是相对少 \end{aligned}$

所以，

如果我们对比原图，就是第一次出现的图像是，会出现，

对于第一个部分，

${\hat{u}}_{0} - {\hat{u}}_{1} = {\hat{y}}_{1} = 1.63$ ${\hat{u}}_{1} - {\hat{u}}_{2} = {\hat{y}}_{2} = - 0.4$

所以，

$\hat{y} = {\hat{y}}_{1} + {\hat{y}}_{2} = 1.63 + (- .4) = 1.24$

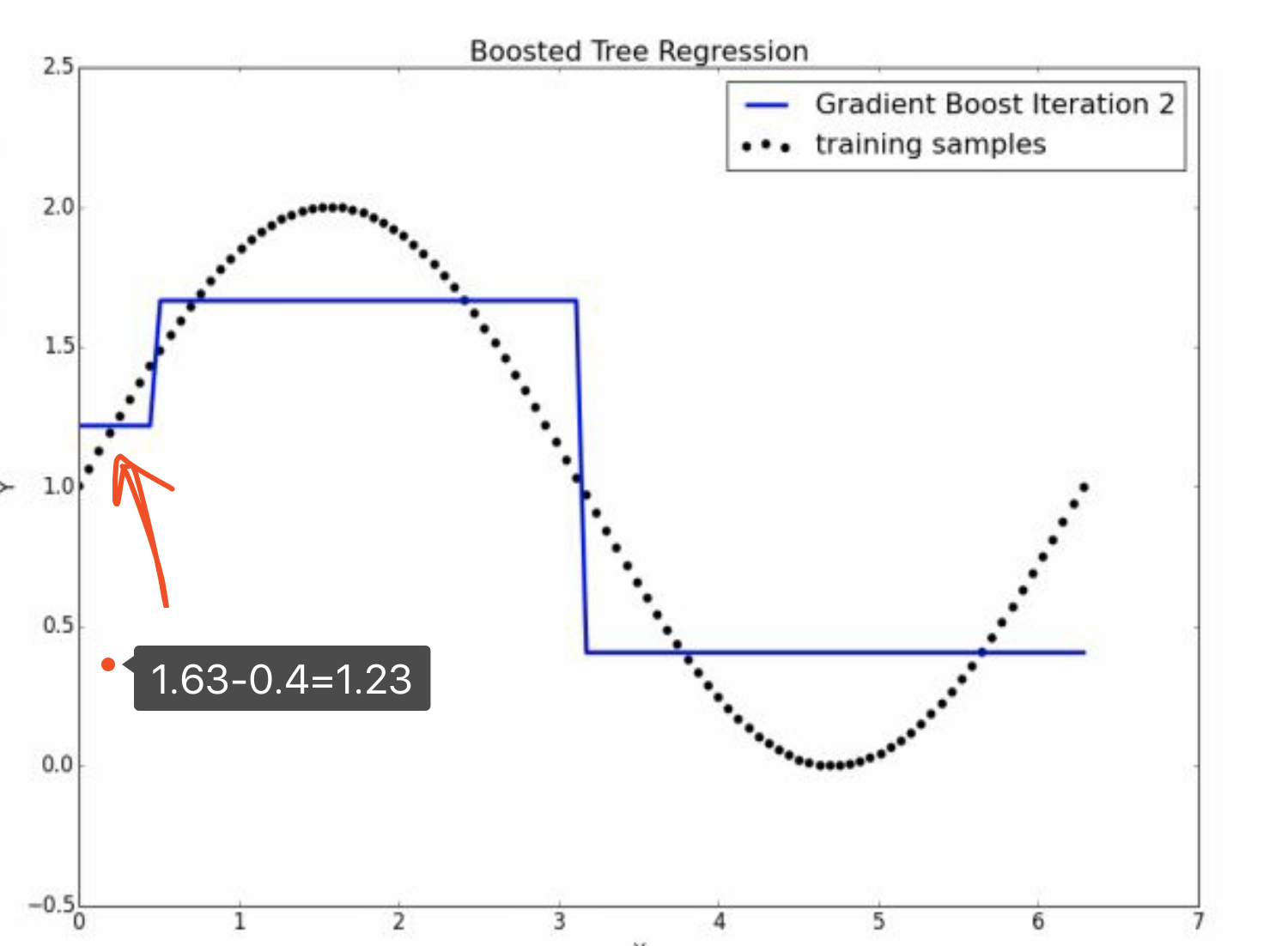
已知，

${\hat{u}}_{1} - {\hat{y}}_{2} (- 0.4) = {\hat{u}}_{2}$

所以 ${\hat{u}}_{2} > {\hat{u}}_{1}$ ，最左边的图像发生上移。

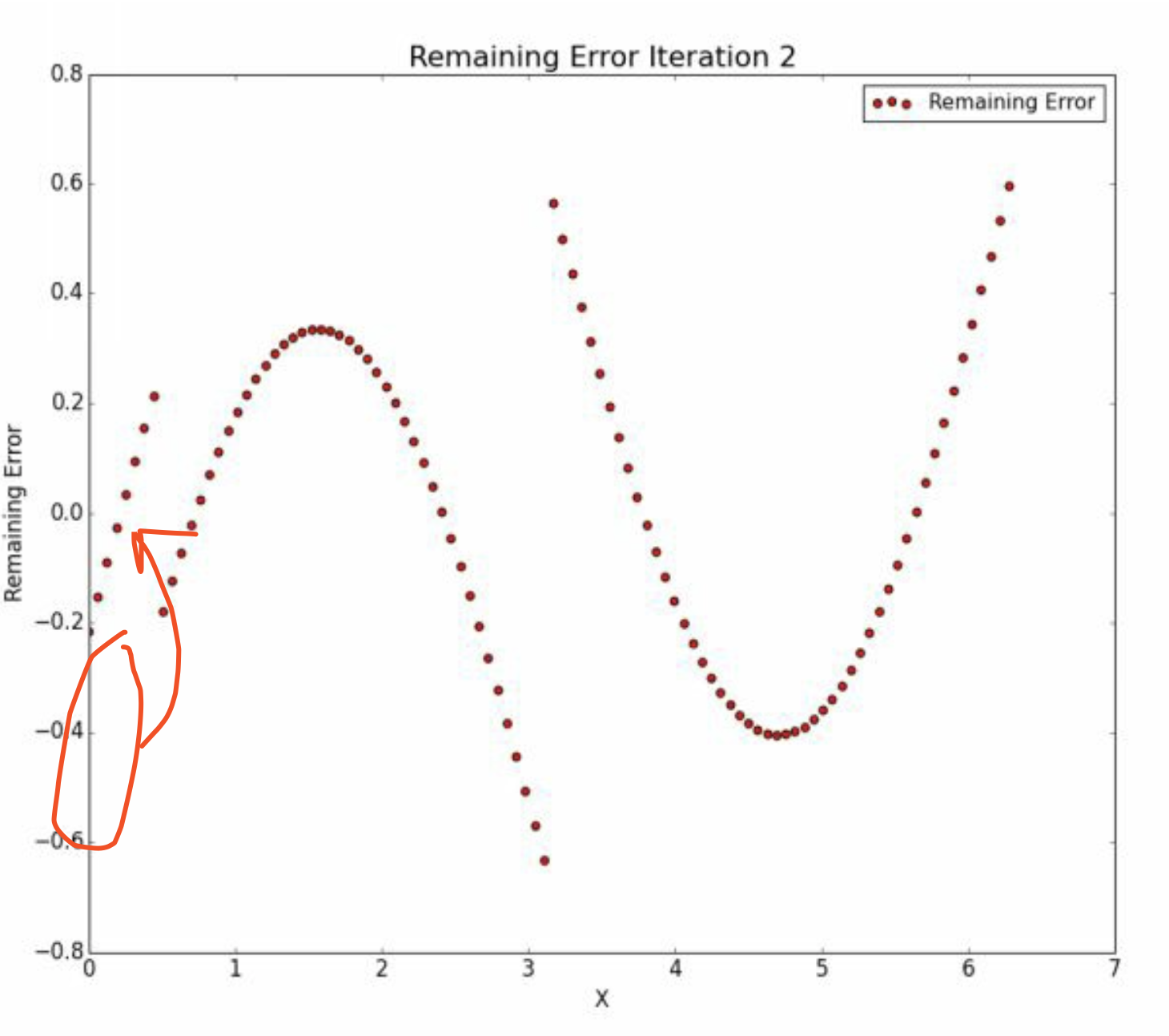
我们知道

${\hat{y}}_{2} (- 0.4) + {\hat{u}}_{2} = {\hat{u}}_{1}$

因此，在 ${\hat{y}}_{2} (- 0.4)$ 和 ${\hat{u}}_{2}$ 的图像中，他们的移动方向相反。

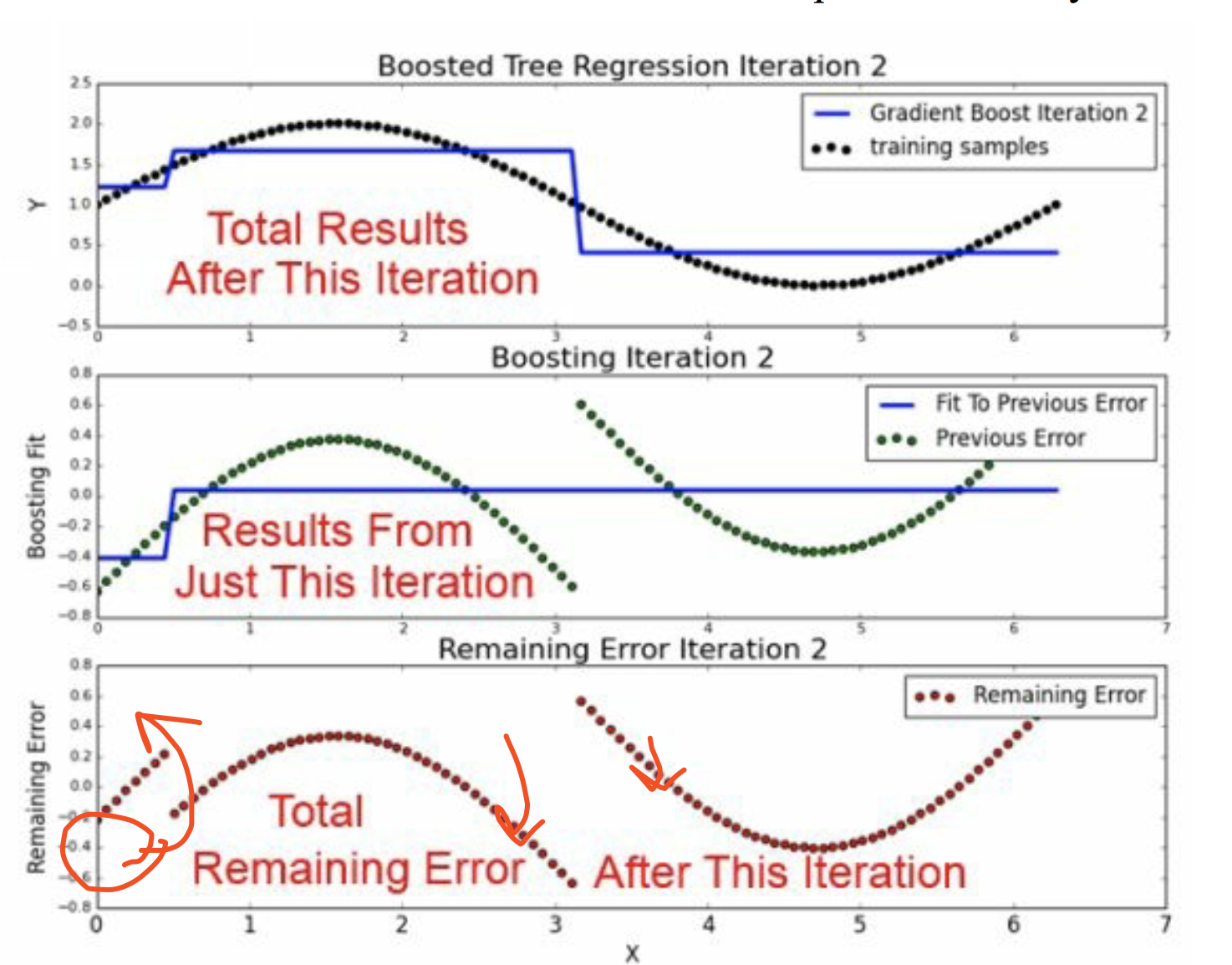
他们之间的变化趋势如图。

5.3 round>=3

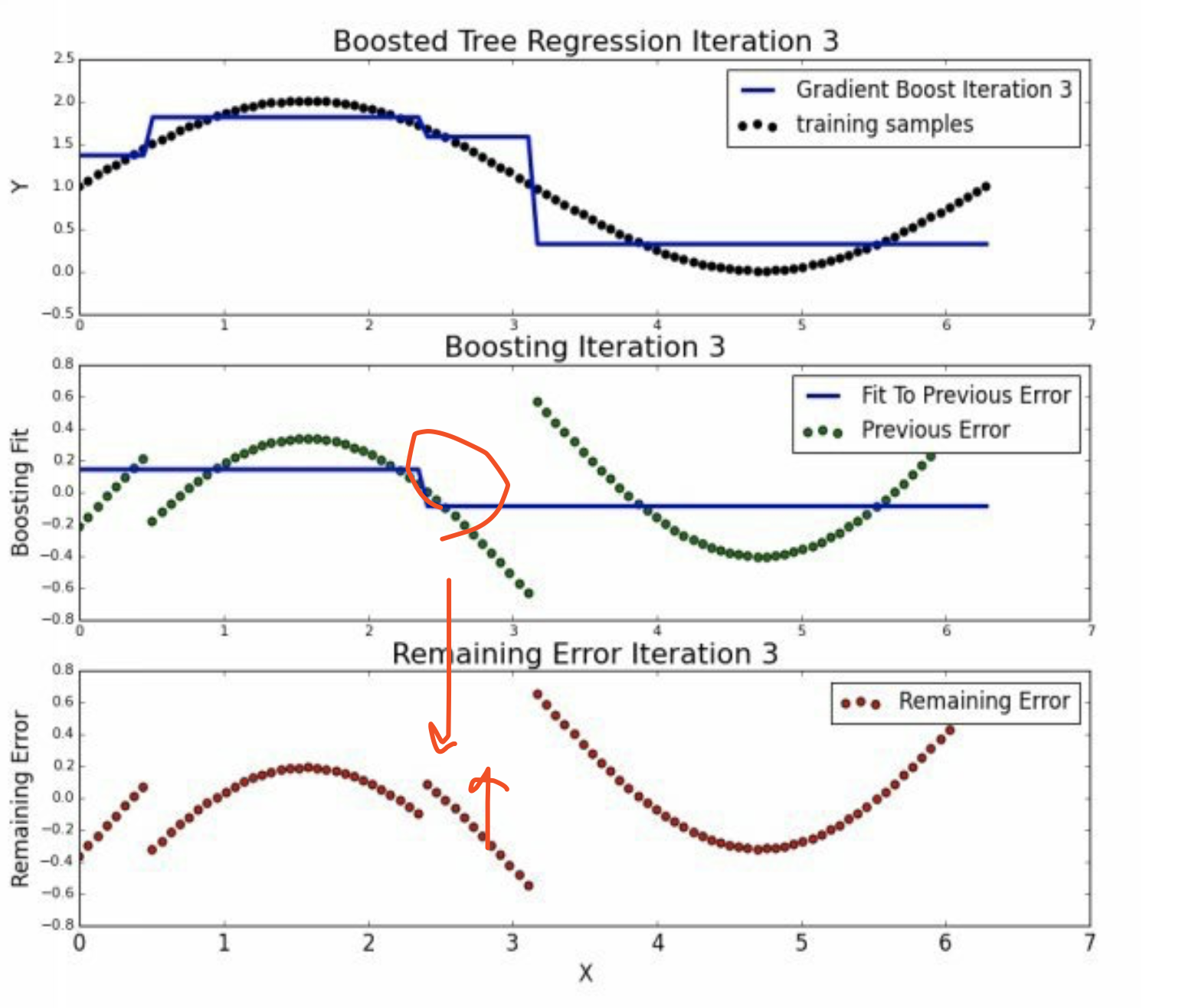
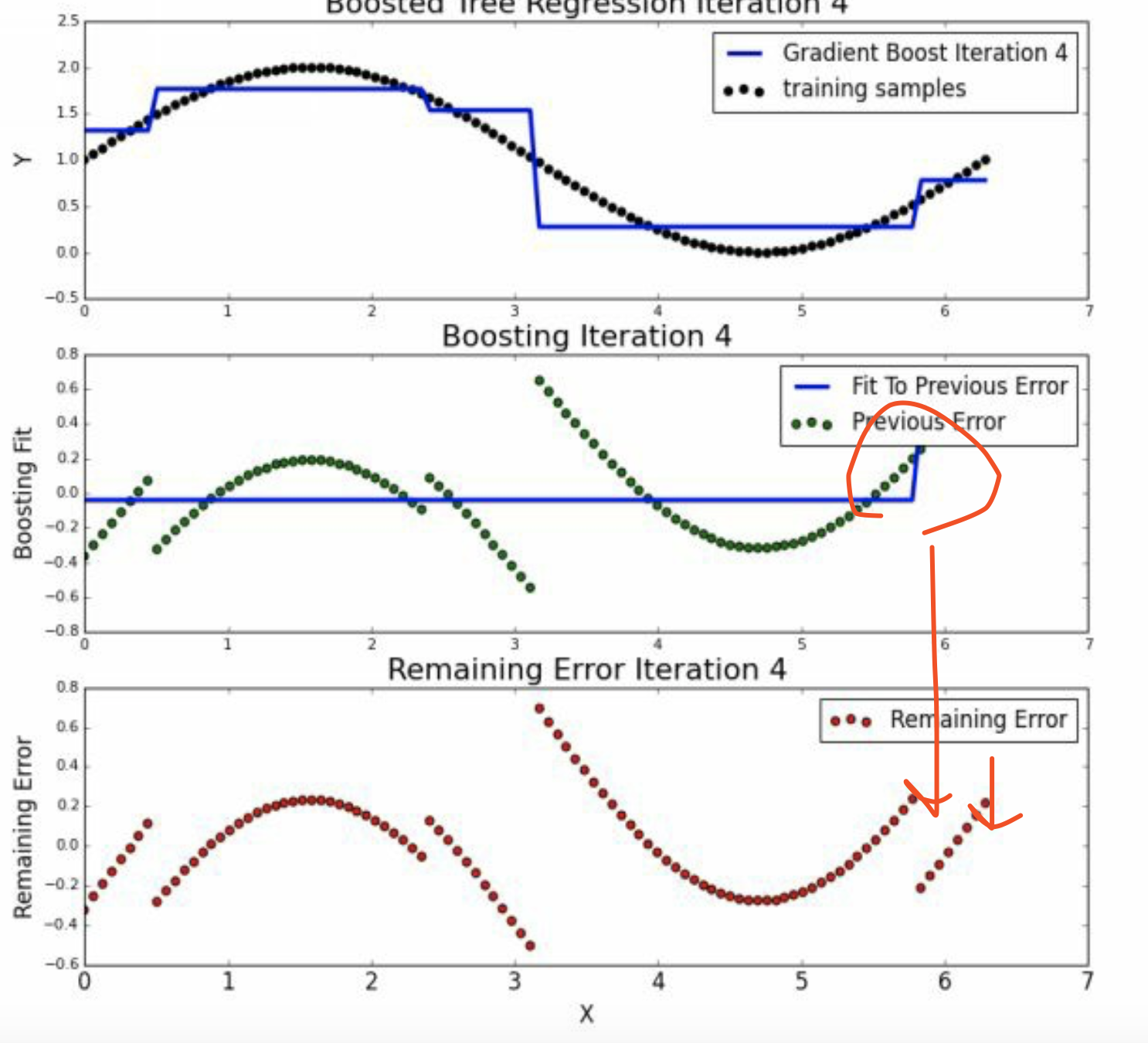
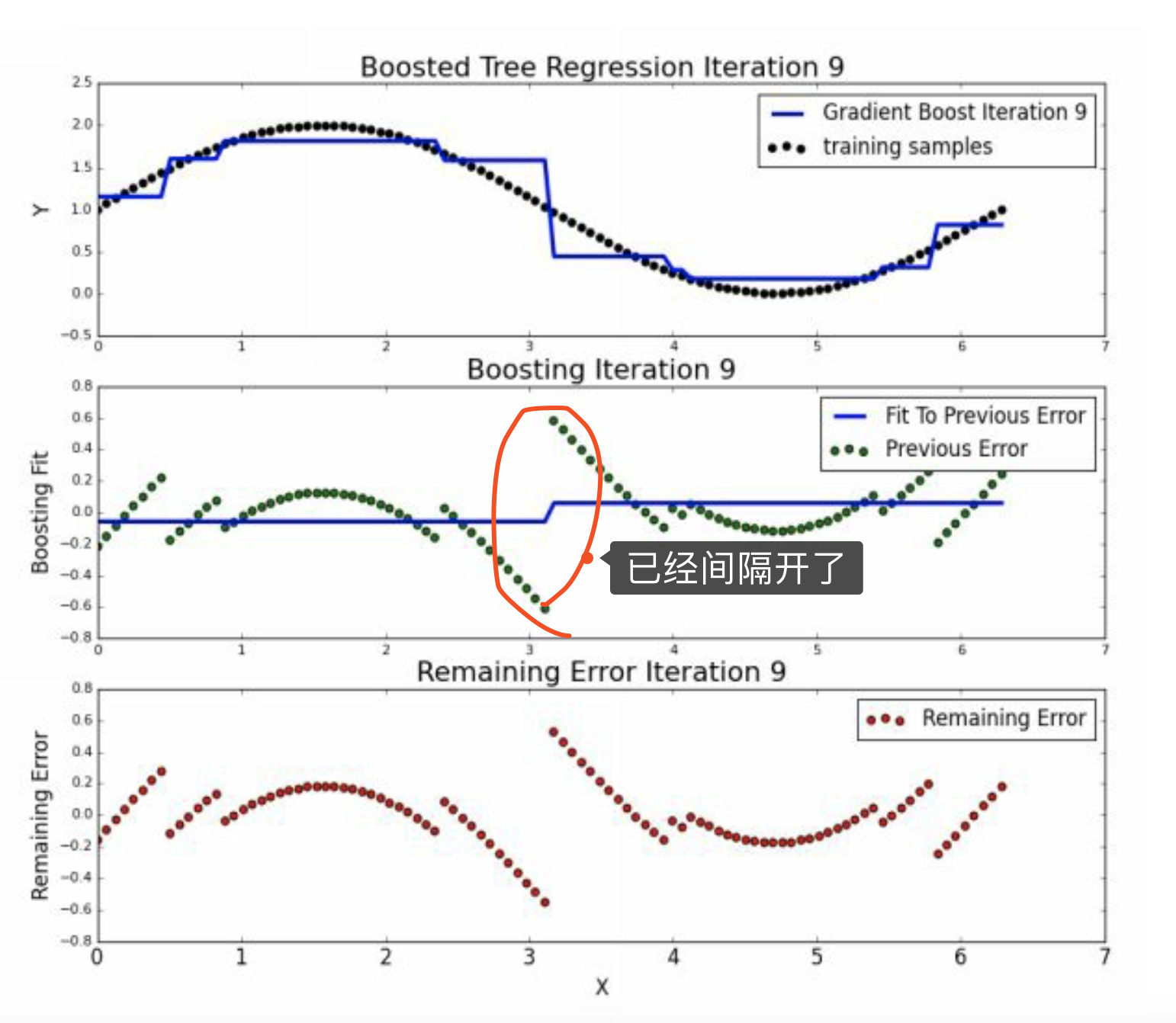
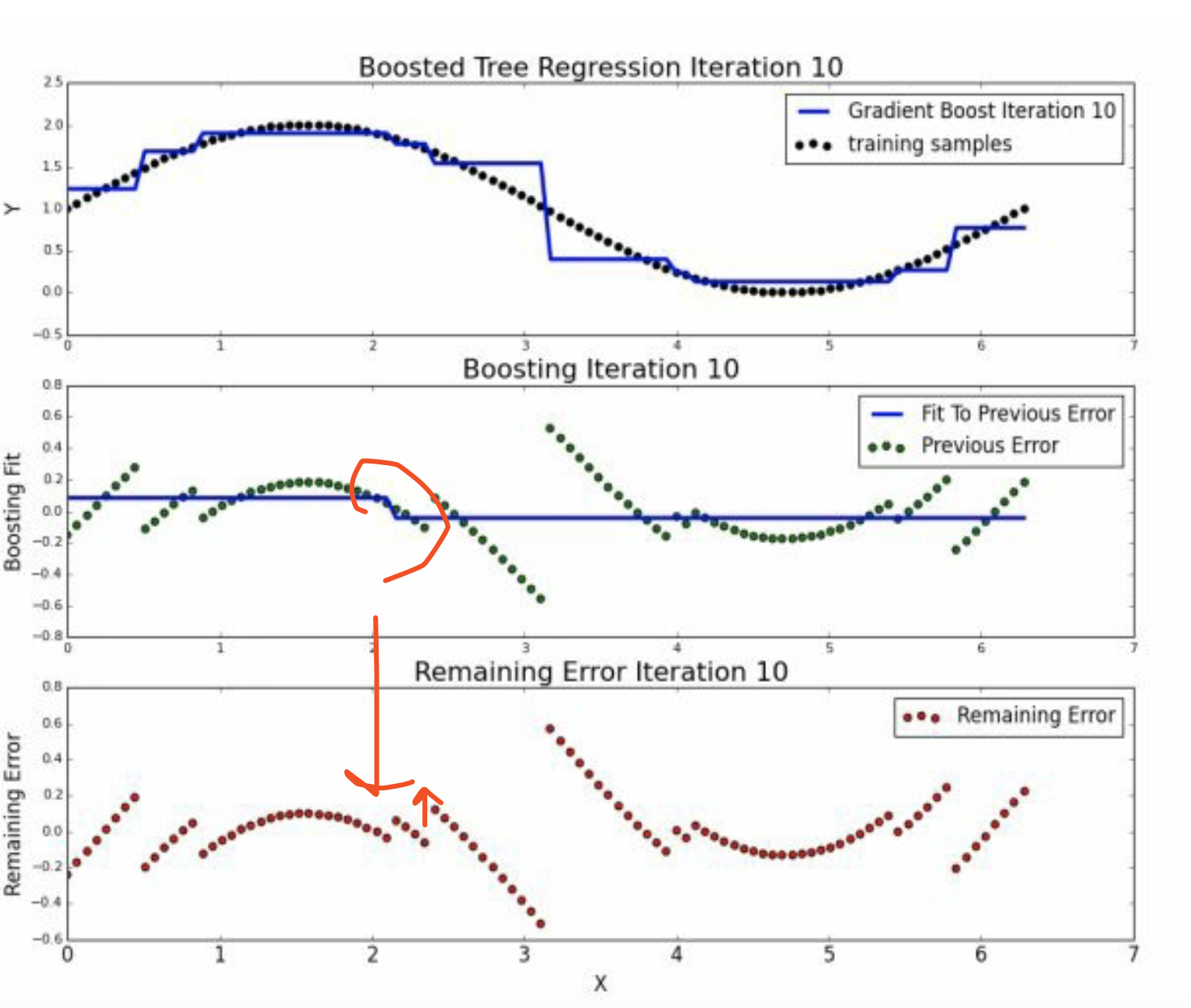
到迭代9和10的时候，基本上已经没有什么切分了。

5.4 depth = 2的精进

以上是depth = 1的方法，迭代到10就没有进步了。 也就是说depth太少，迭代没有意义。

这个时候可以增加depth，也就是每次决策树要 跑慢一点。

好处就是因为一刀两半，两层就是四半了，更佳精密。满足 $2^{d e p t h}$ 的关系。

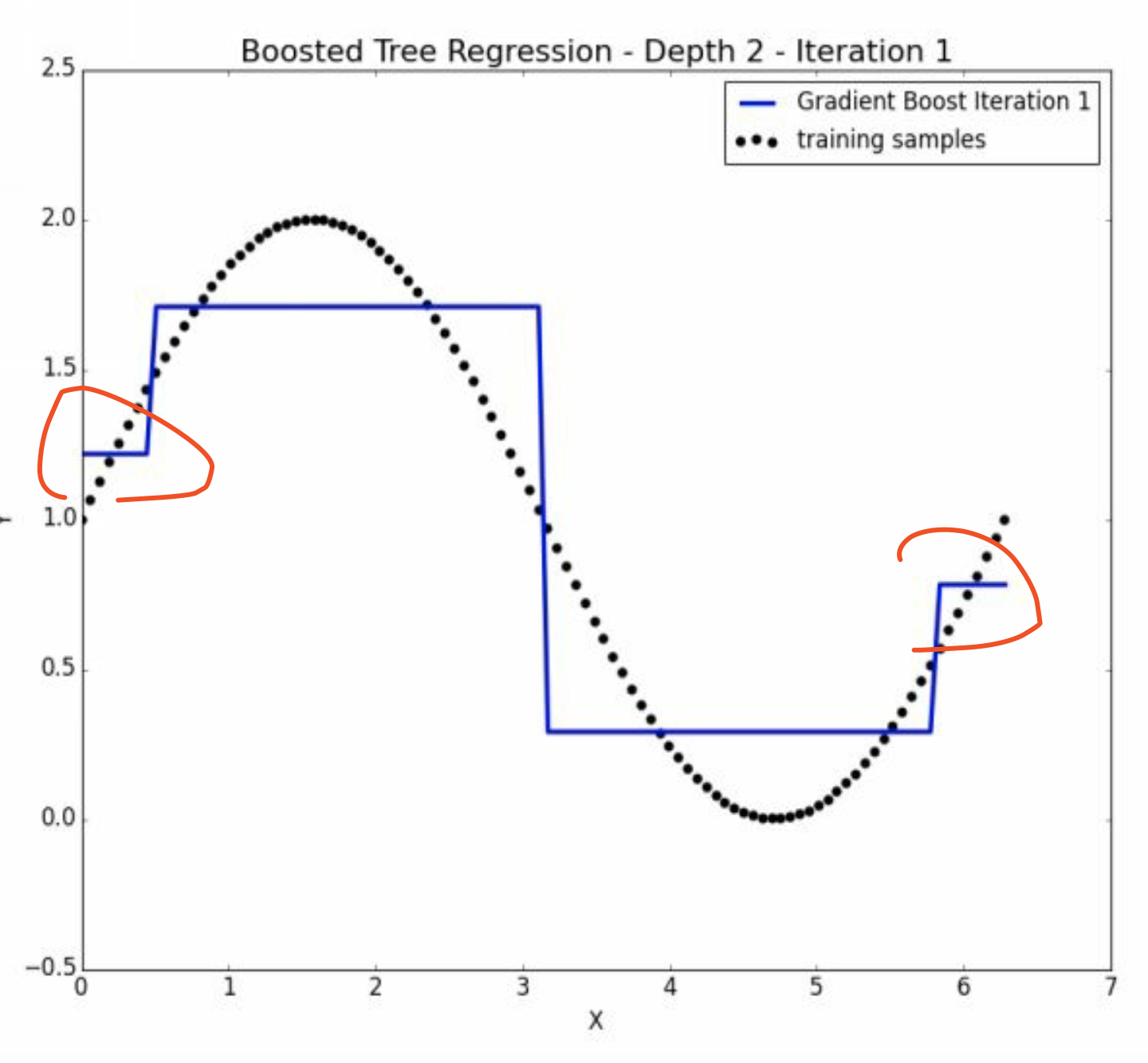
显然虽然depth=2单次时间长了，因为层级多了，但是理论上迭代的也少了。

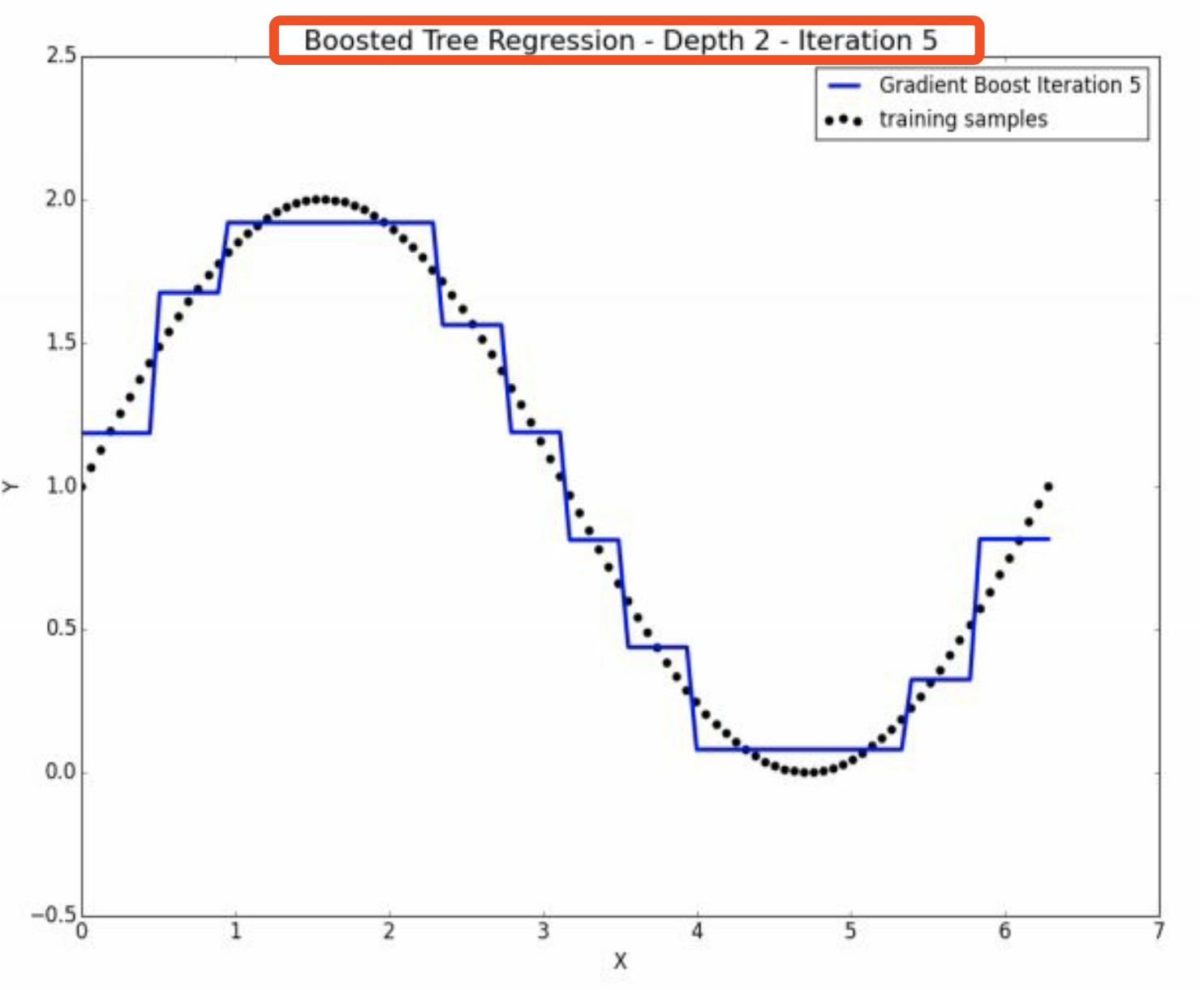
但是实际上还是depth多的好，如图，这是5次迭代depth=2的情况。

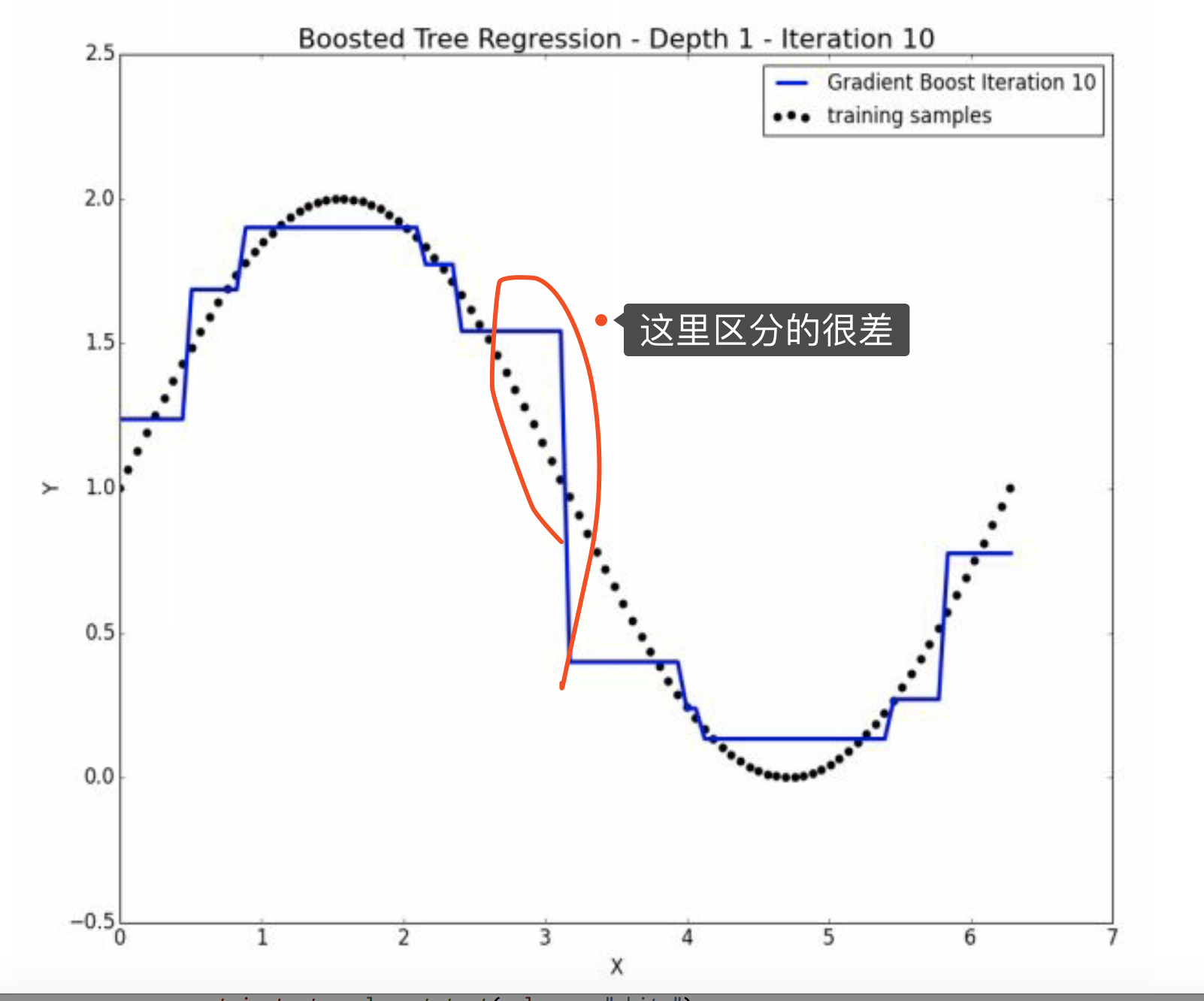
这是10次depth=1的情况。

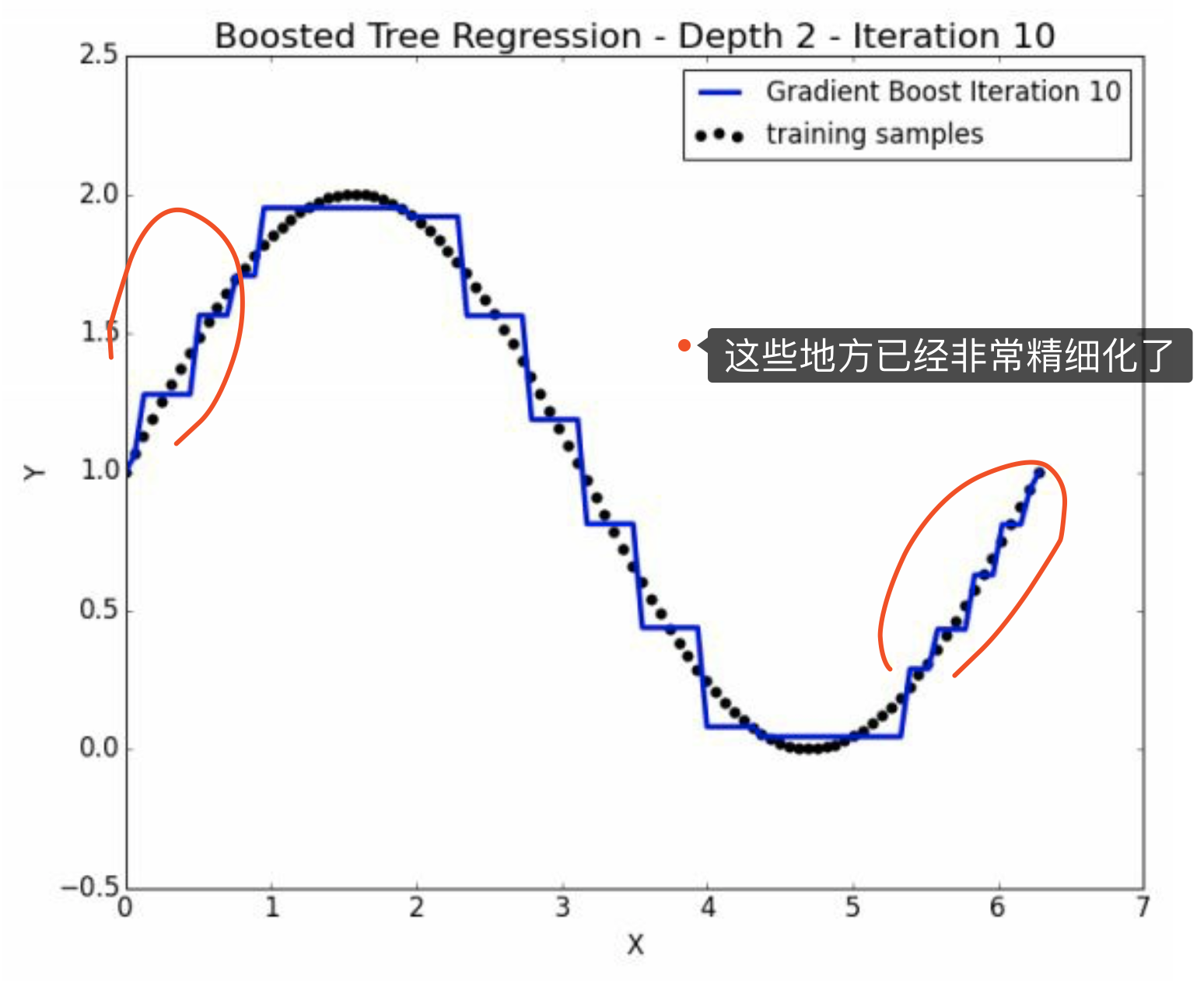
这是10次depth=2的情况。已经非常精细化了。

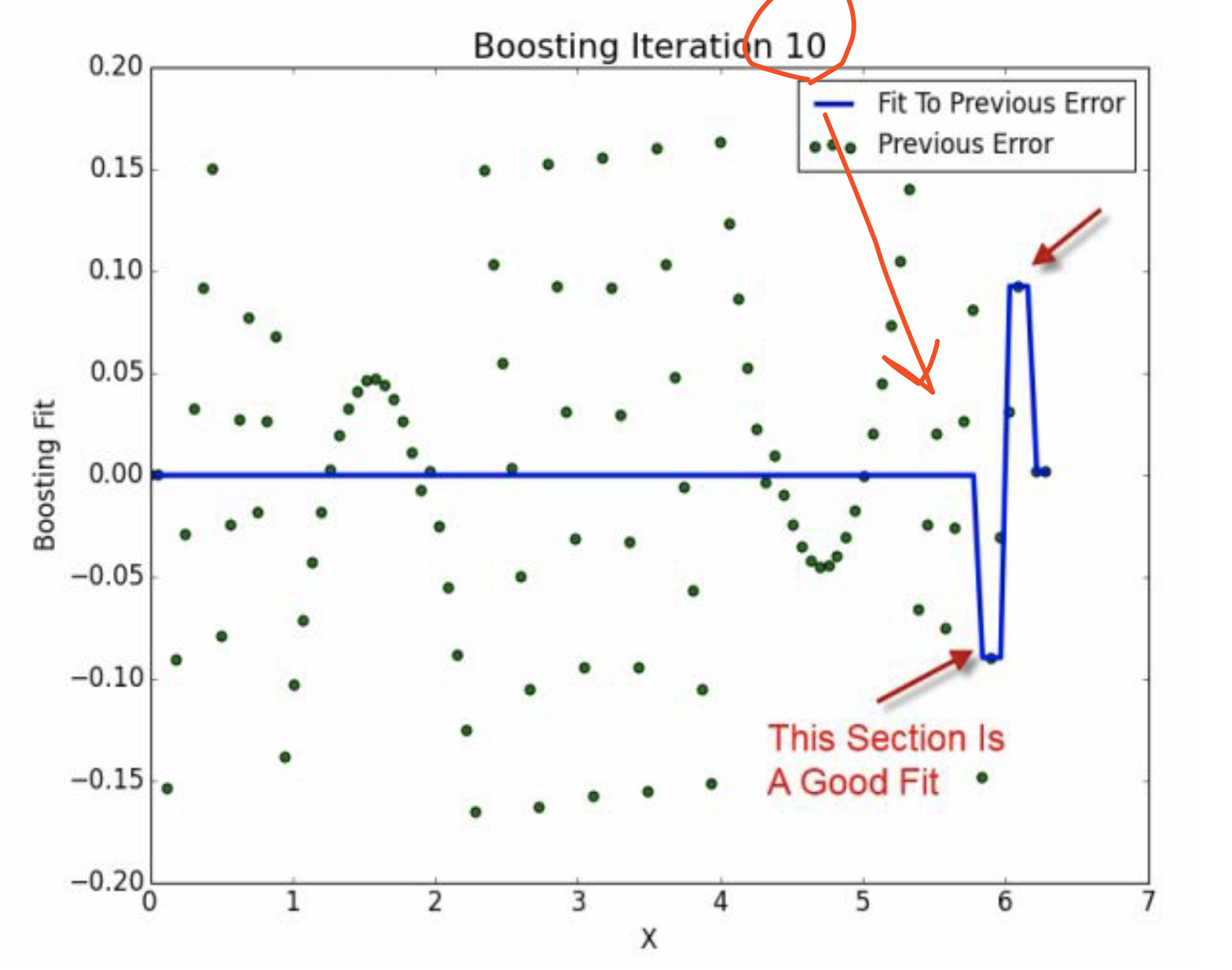
这恰好说明了。第十次迭代虽然整体上是weak的，但是是某方面的专家。并且注意，其他地方的 $\hat{y} = 0$ 。 因此，没有使得其他地方变差。

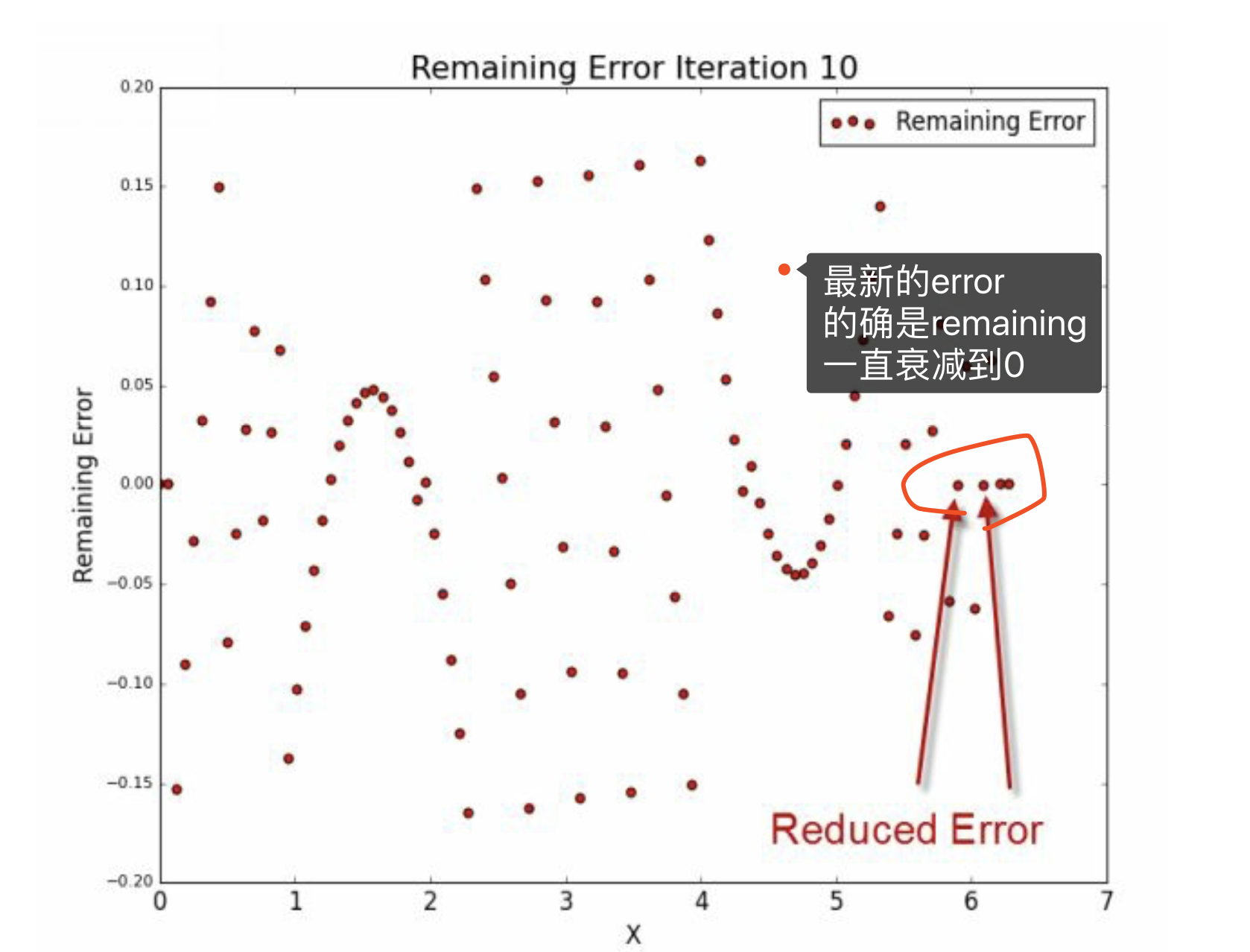
上图是 $\hat{u}$ 的变化情况，理论上就是要衰减到0。

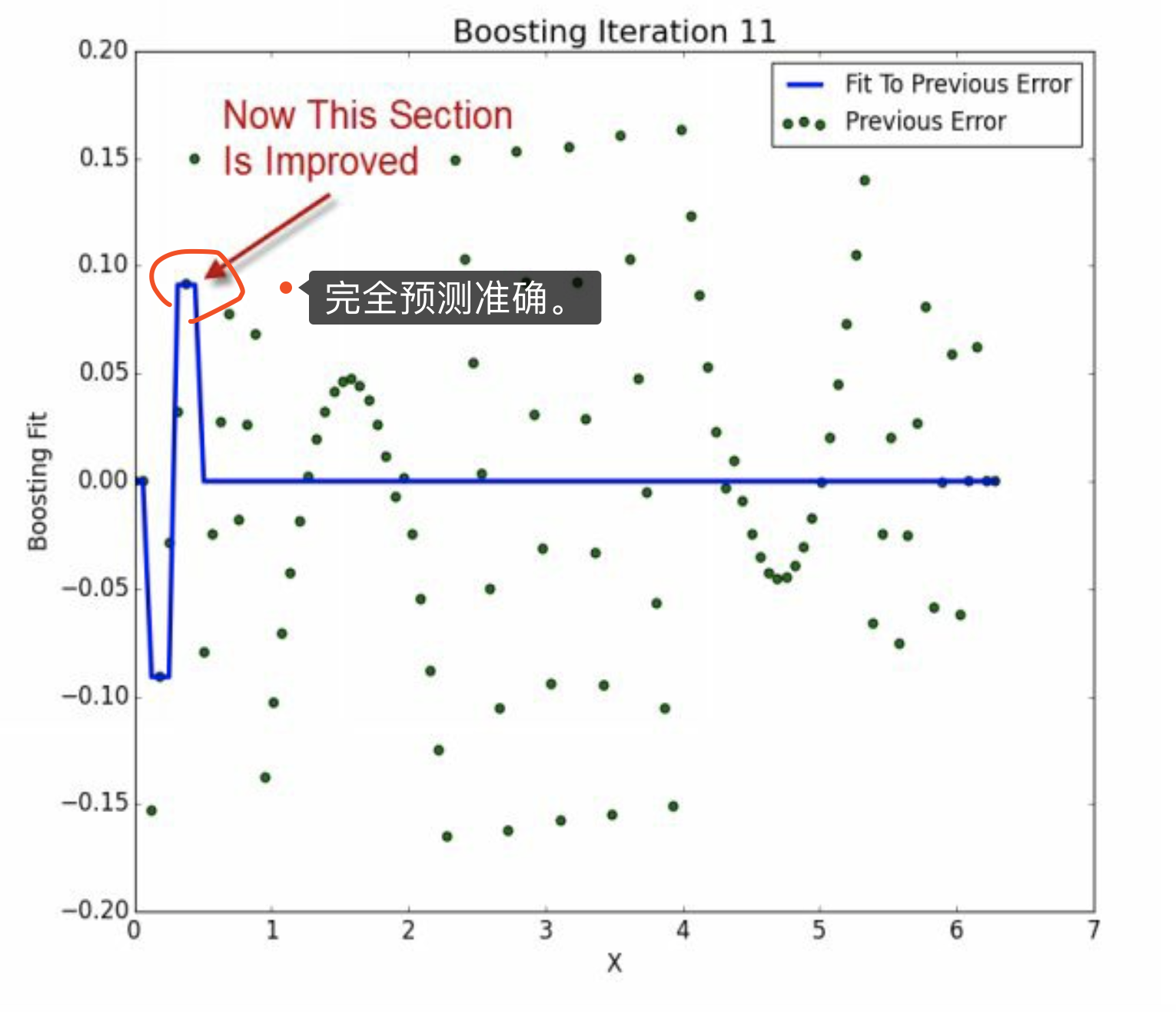
第11次迭代，完全预测准确，

${\hat{u}}_{i - 1} - {\hat{u}}_{i} = {\hat{y}}_{i}$

当 ${\hat{u}}_{11} = {\hat{y}}_{12}$ ，那么 ${\hat{u}}_{12} = 0$ 。

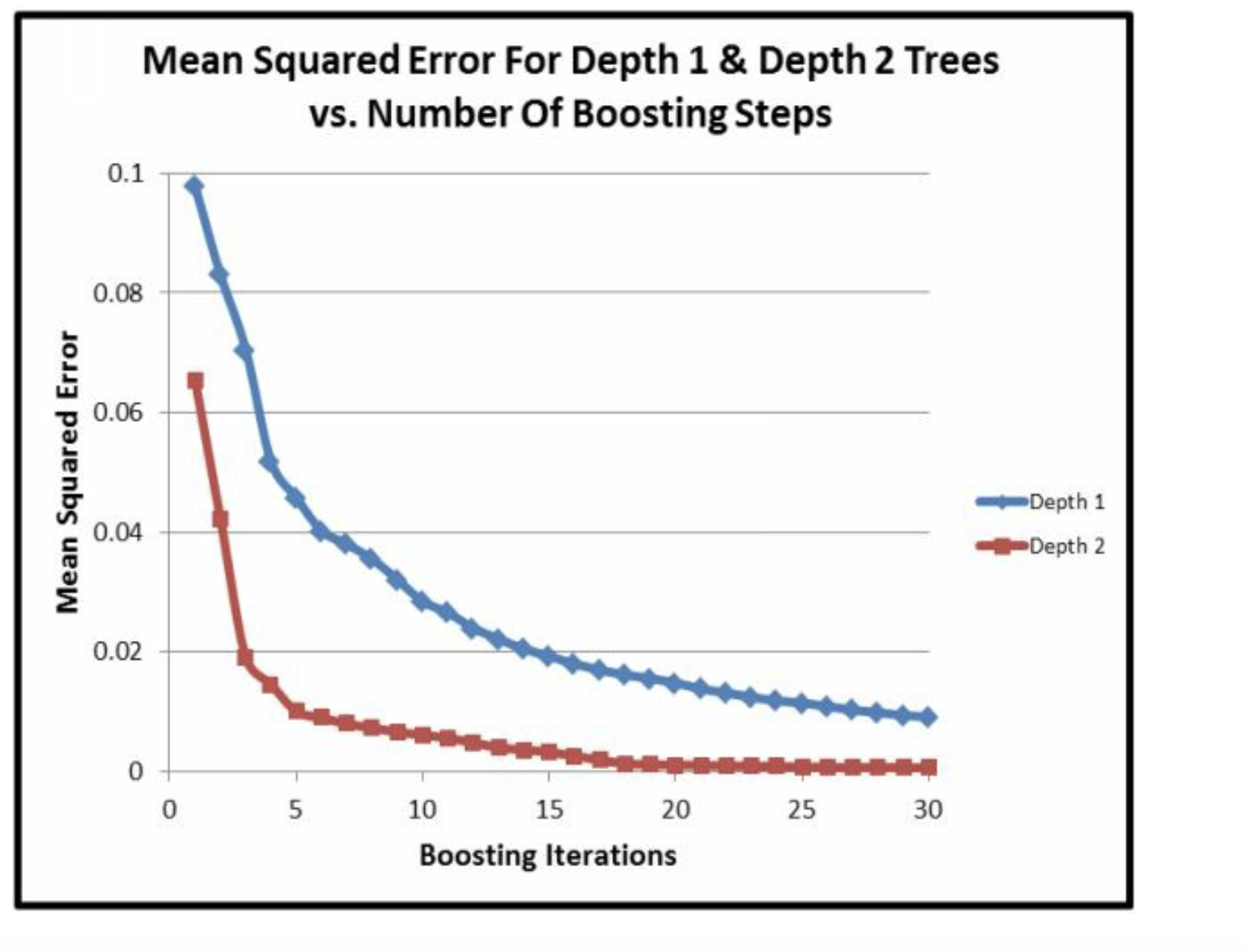
这里给出了证明rmse的确是depth=2降低的快。

总结

depth设置太小了，很影响拟合效果。一般sklearn是depth=3的默认值。

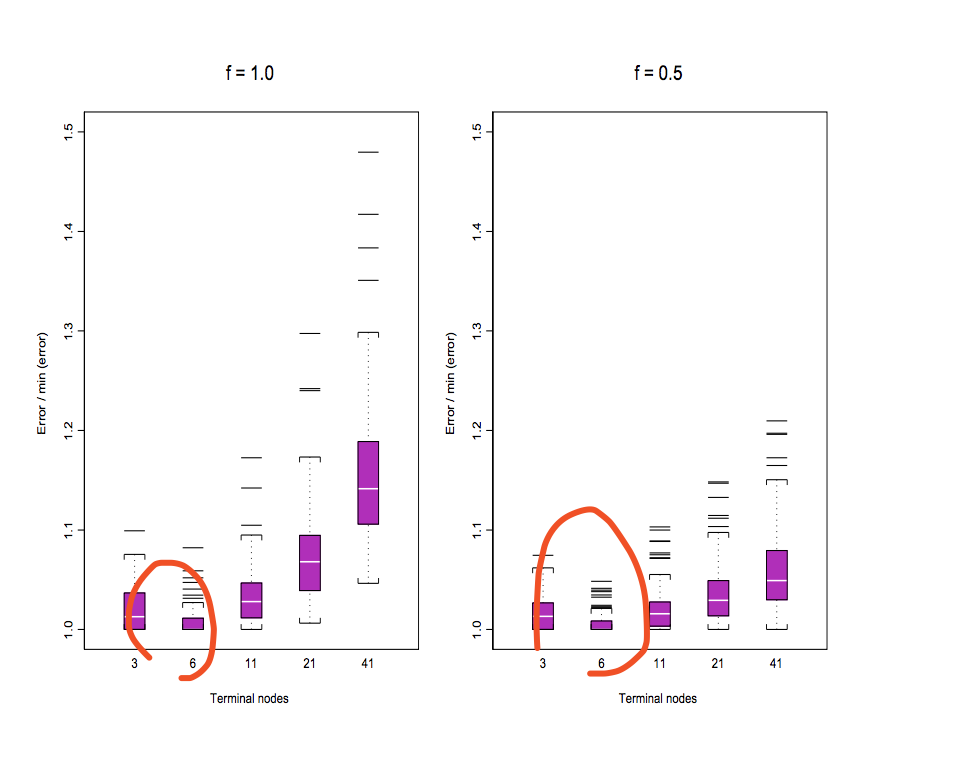
这篇文献论证了nodes=6比多的好。

6 学习率

学习率越大，表示迭代越快，步子越大。

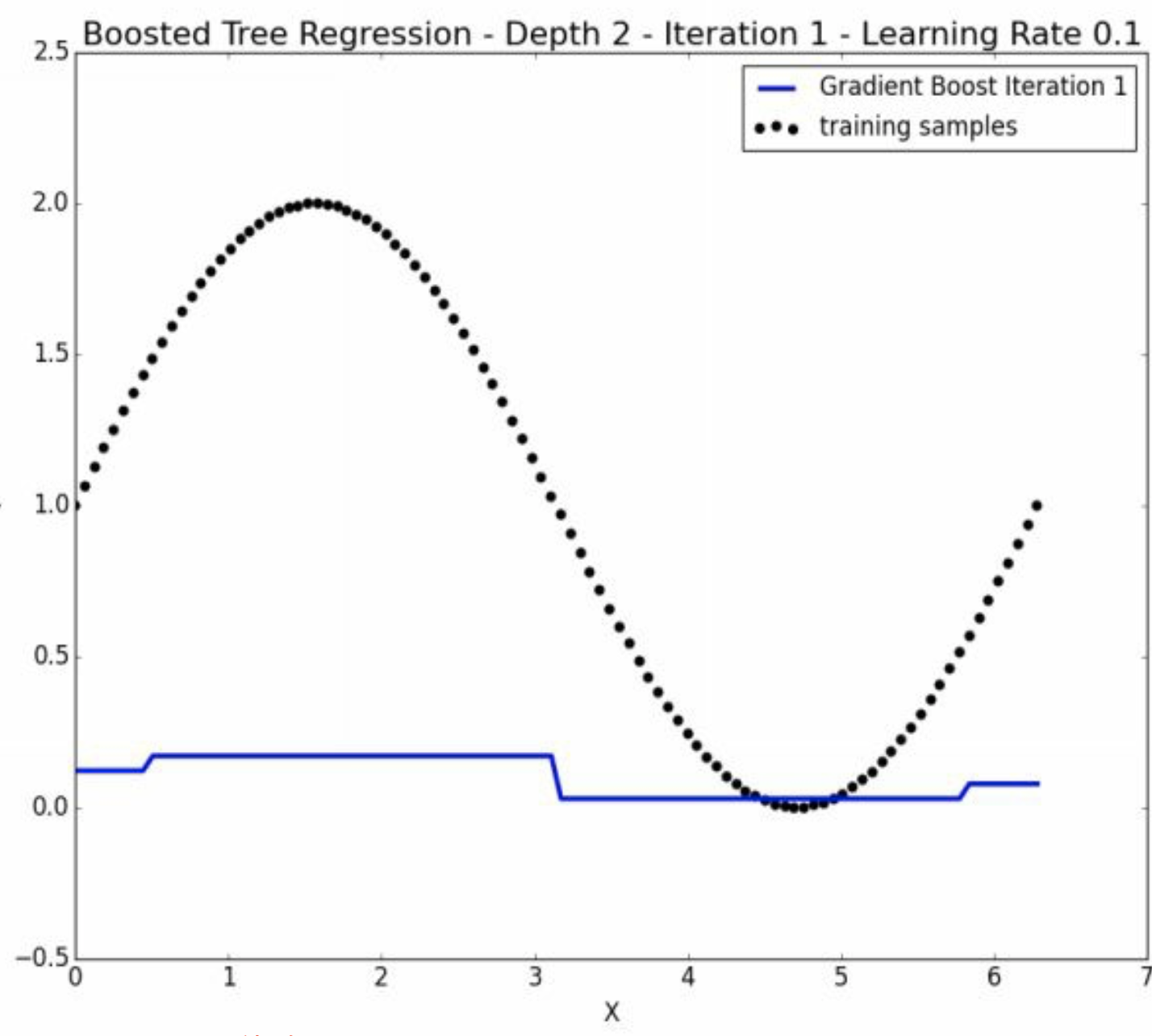
这里注意第一步 ${\hat{u}}_{0} \cdot α = {\hat{y}}_{1}$ ，因此修改了learning rate，需要修改nrounds 很直观！！！ nrounds就更加慢了。

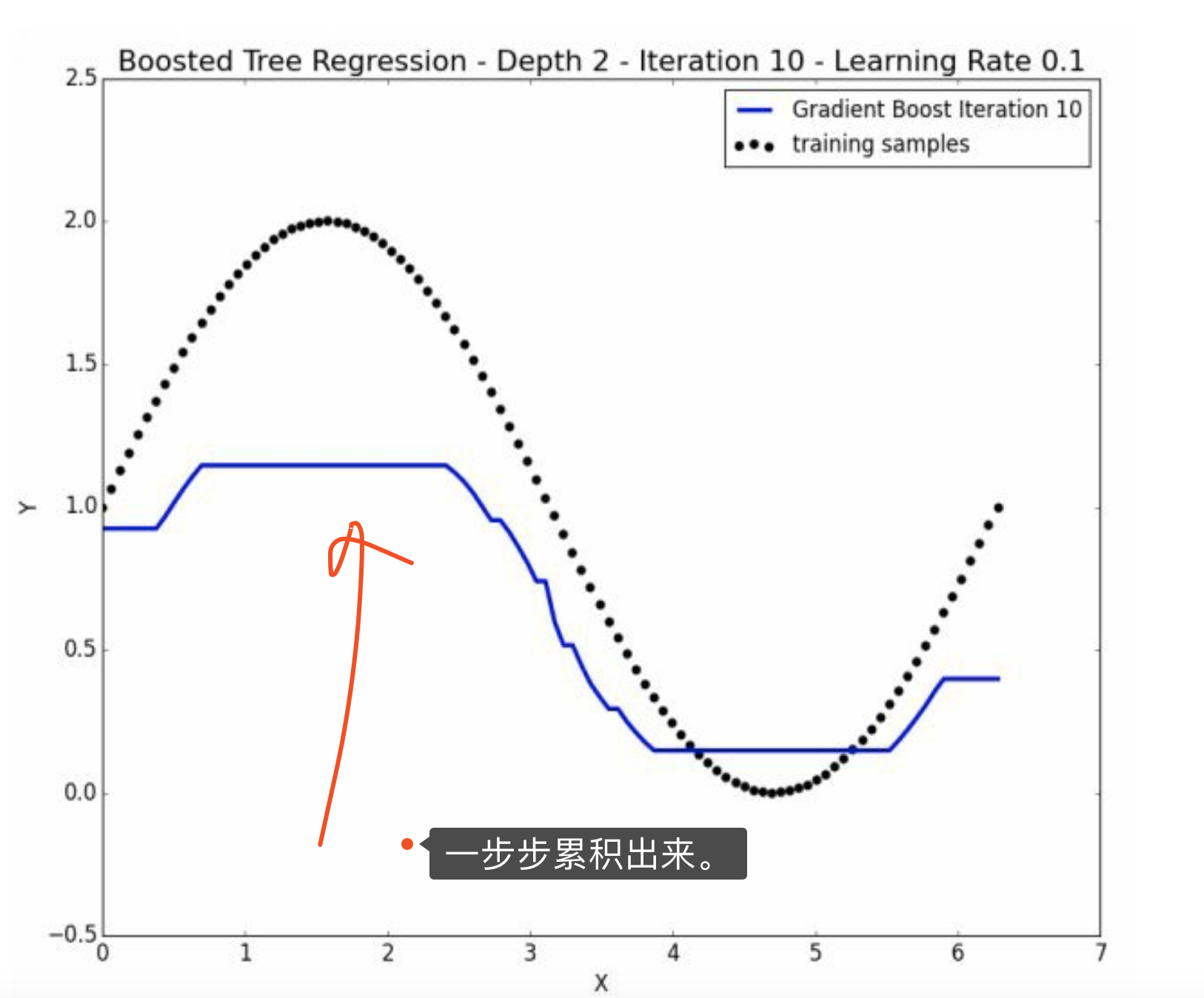
因此存在

$α \cdot ({\hat{u}}_{0} - {\hat{u}}_{1}) = {\hat{y}}_{1}$

这里就是说，实际上每次的错误， ${\hat{y}}_{1}$ 只吸收 $α$ ，还有 $1 - α$ 不吸收，但是随着迭代数量增加，会慢慢吸收的。

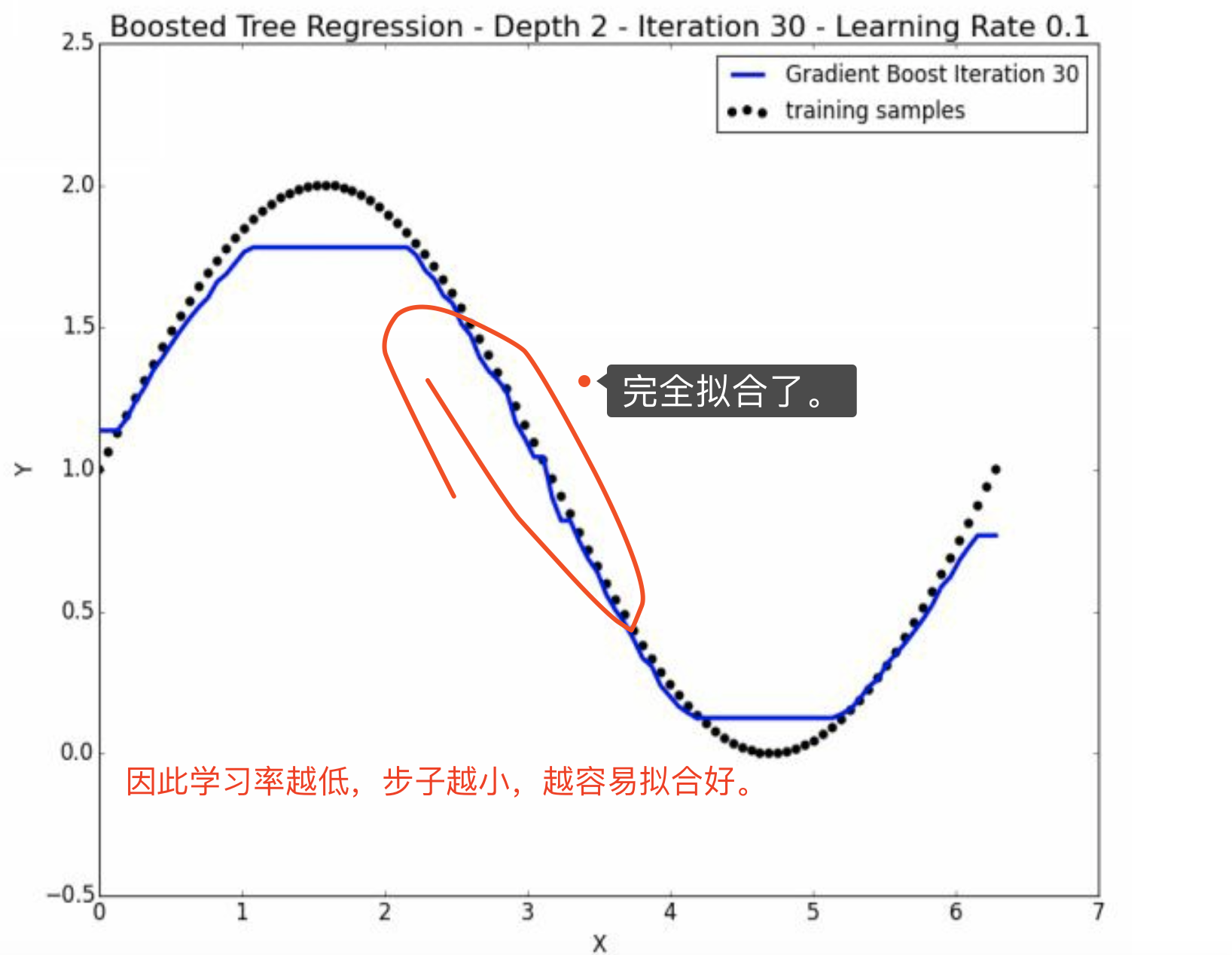
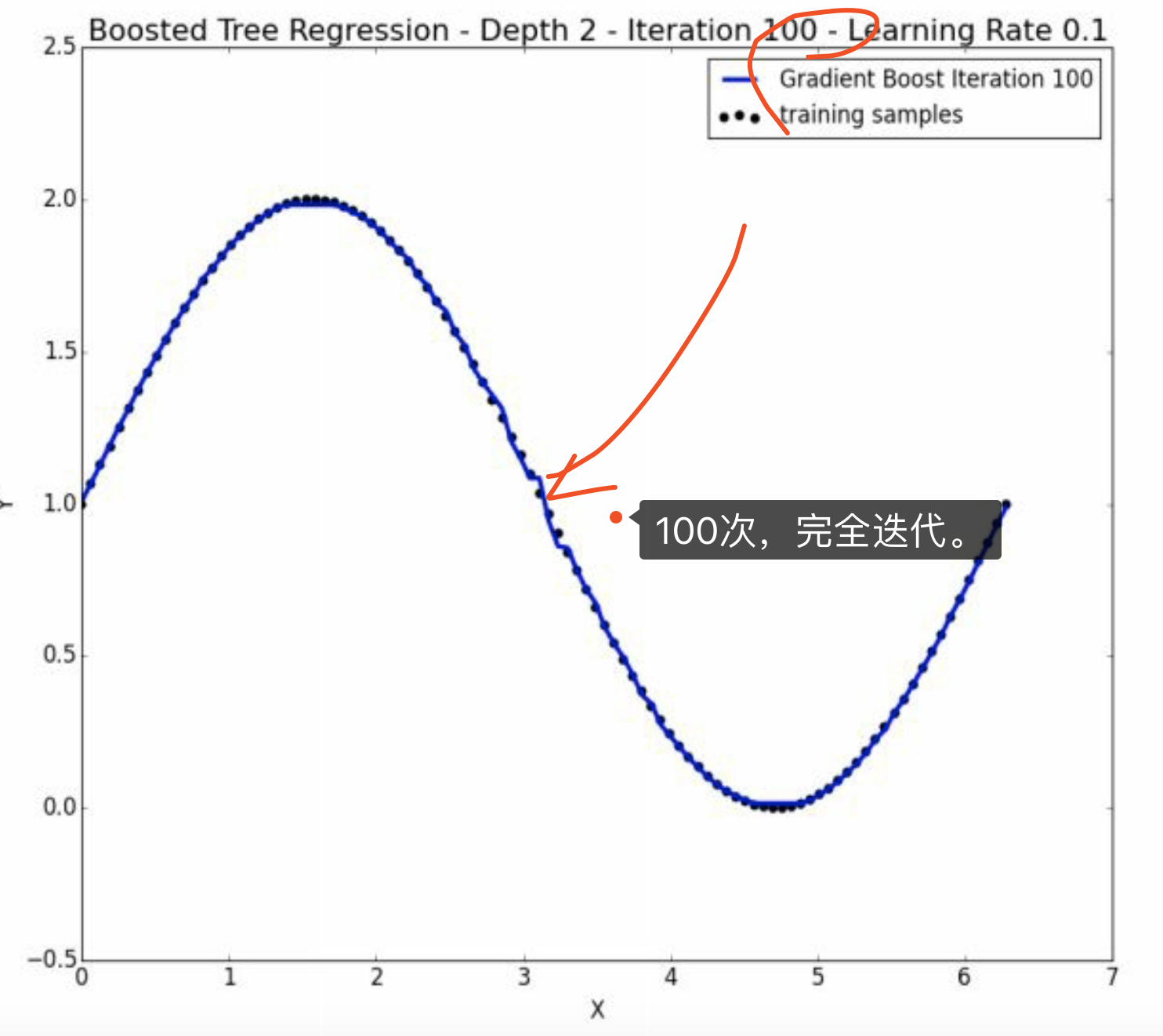
6.1 对overfitting加深理解

显然学习率下降后，更加慢，模型更加拟合、代表训练组。但是如果训练组中包含了error或者noise，那么训练组就不能代表整体样本了，这就是 过拟合 。

全信 -> overfitting
不信 -> under-fitting
要学会独立思考

error客观存在的，因此反而这个时候y-y_hat = 0 不是好事情了，说明y_hat captures noise.

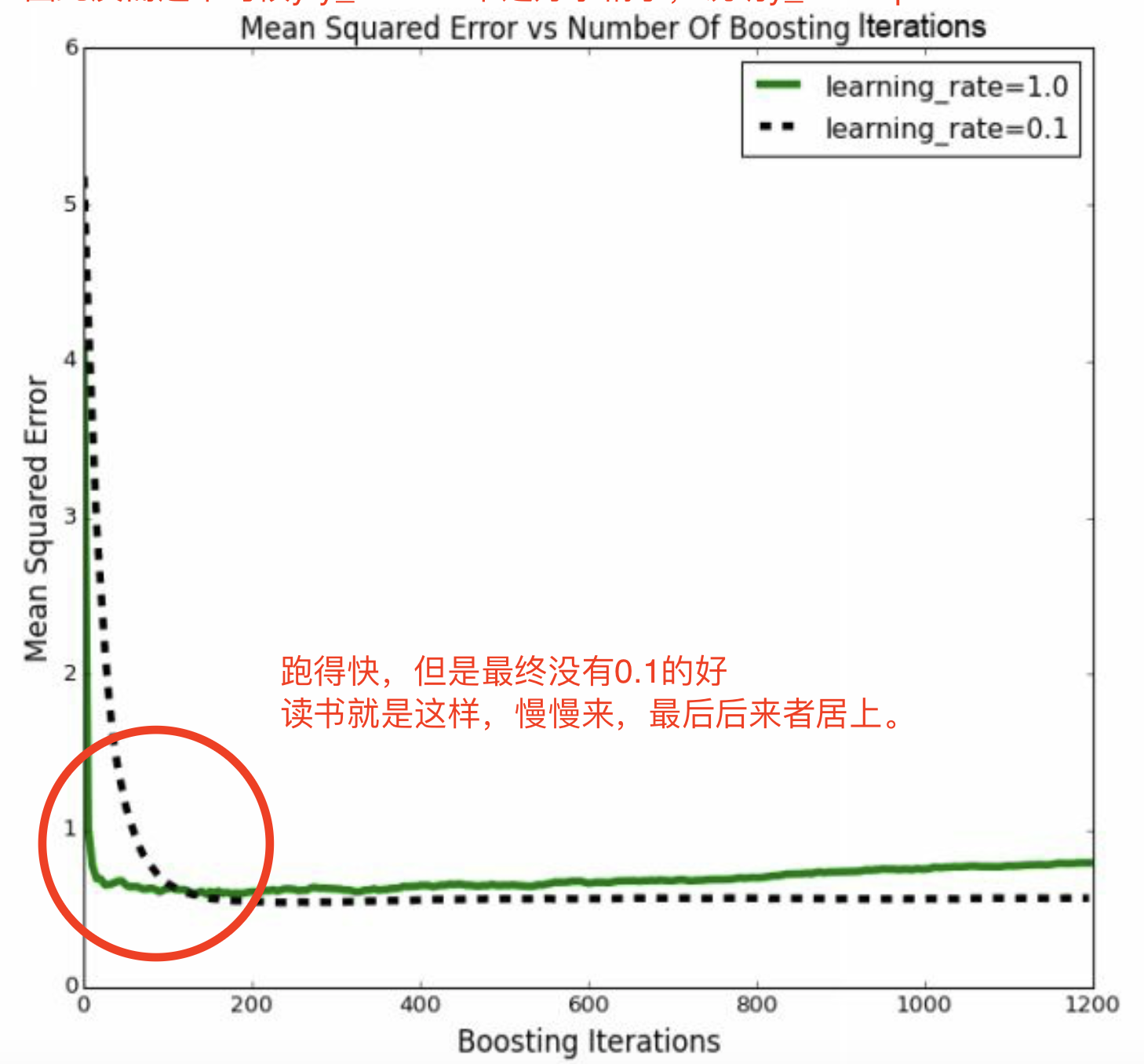
因此，就是说，步子大了，不好。因为可能是噪音导致的，以下就冲出轨道了。因此，慢慢来，虽然耗时间，但是不会出错。

跑得快，但是最终没有0.1的好读书就是这样，慢慢来，最后后来者居上。

6.2 $α \in [0, 1]$

之前论述，

$α \cdot ({\hat{u}}_{0} - {\hat{u}}_{1}) = {\hat{y}}_{1}$

如果 $α > 1$ 就是在扩大误差。
如果 $α < 0$ 就是在往反方向。

7 进行一定的总结

可知，

${\hat{u}}_{i - 1} - {\hat{y}}_{i} = {\hat{u}}_{i}$

我们发现，就是上一期的误差 ${\hat{u}}_{i - 1}$ ，也就是说从 $y = {\hat{u}}_{0}$ 开始，不断的剪去平均数，直到 ${\hat{y}}_{i} \to {\hat{u}}_{i - 1}$ 为止，也就是 ${\hat{u}}_{i} \to 0$ 。其中，这种之后 ${\hat{u}}_{i} \to 0$ 的，之后的 ${\hat{y}}_{i + 1}$ 也是 $\to 0$ ，所以 ${\hat{u}}_{i + 1} \to 0$ 的。因此，满足稳定的迭代关系。后面哪些 ${\hat{u}}_{i + 1} \neq 0$ 的会被针对，区别对待，特别的锤。

并且会锤的很猛，因为损失函数决定了，是以RMSE来结算，那么在此之前， ${\hat{u}}_{i} = 10$ 和 ${\hat{u}}_{i} = 5$ ，会被 $= 10^{2} : 5^{2} = 4 : 1$ 的倍数对待，前者被使劲锤。

当然AdaBoost，是把对的样本比例放小，错的样本比例放大。因此，默认的GBM，各个样本比例是均分的，都为1.

8 classification using boosting理解

先用最详细的讲法讲，然后总结两次，相当于复习。

8.1 总结1

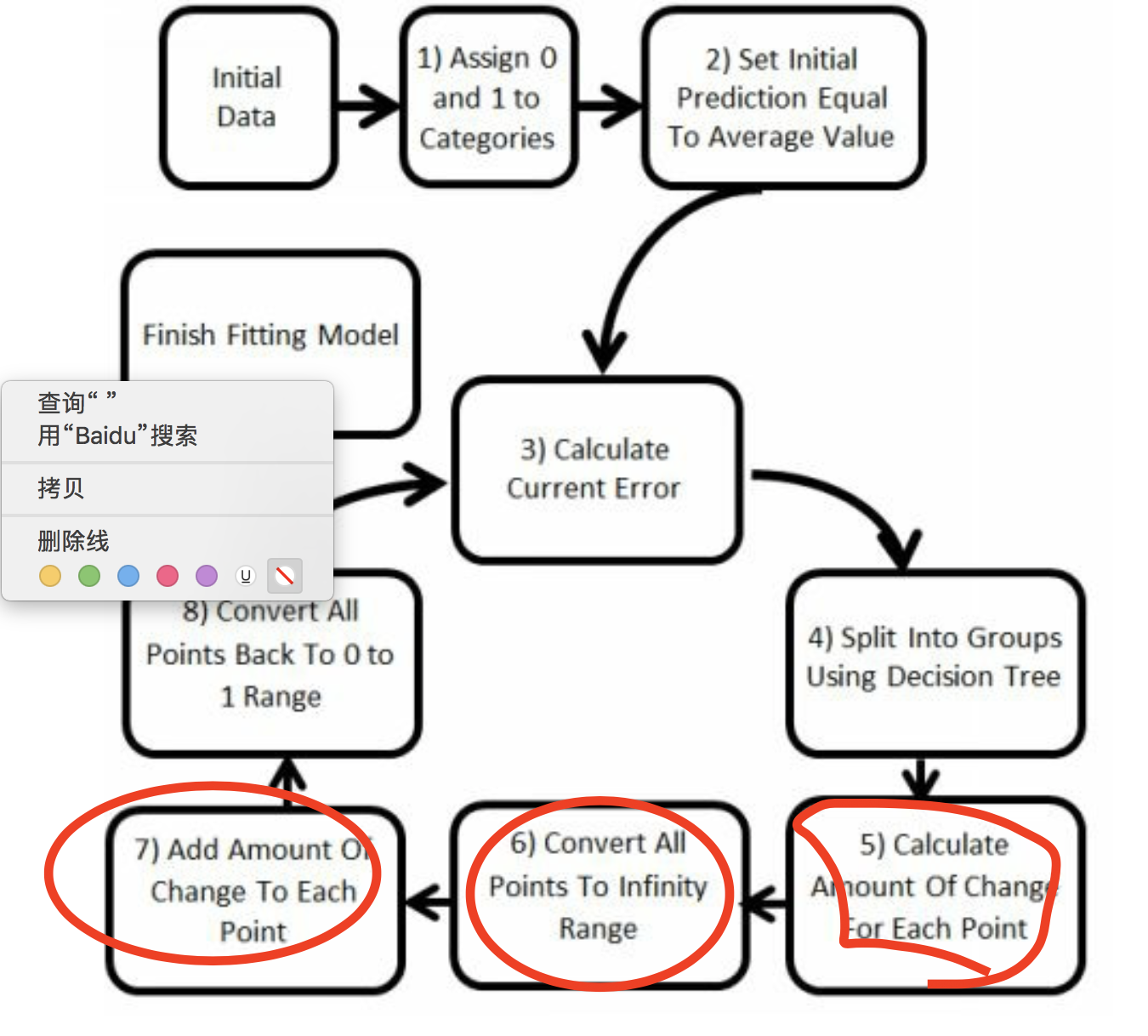
我们发现多了5、6、7步骤，这是因为引入了转换函数logit函数和反函数expit函数。

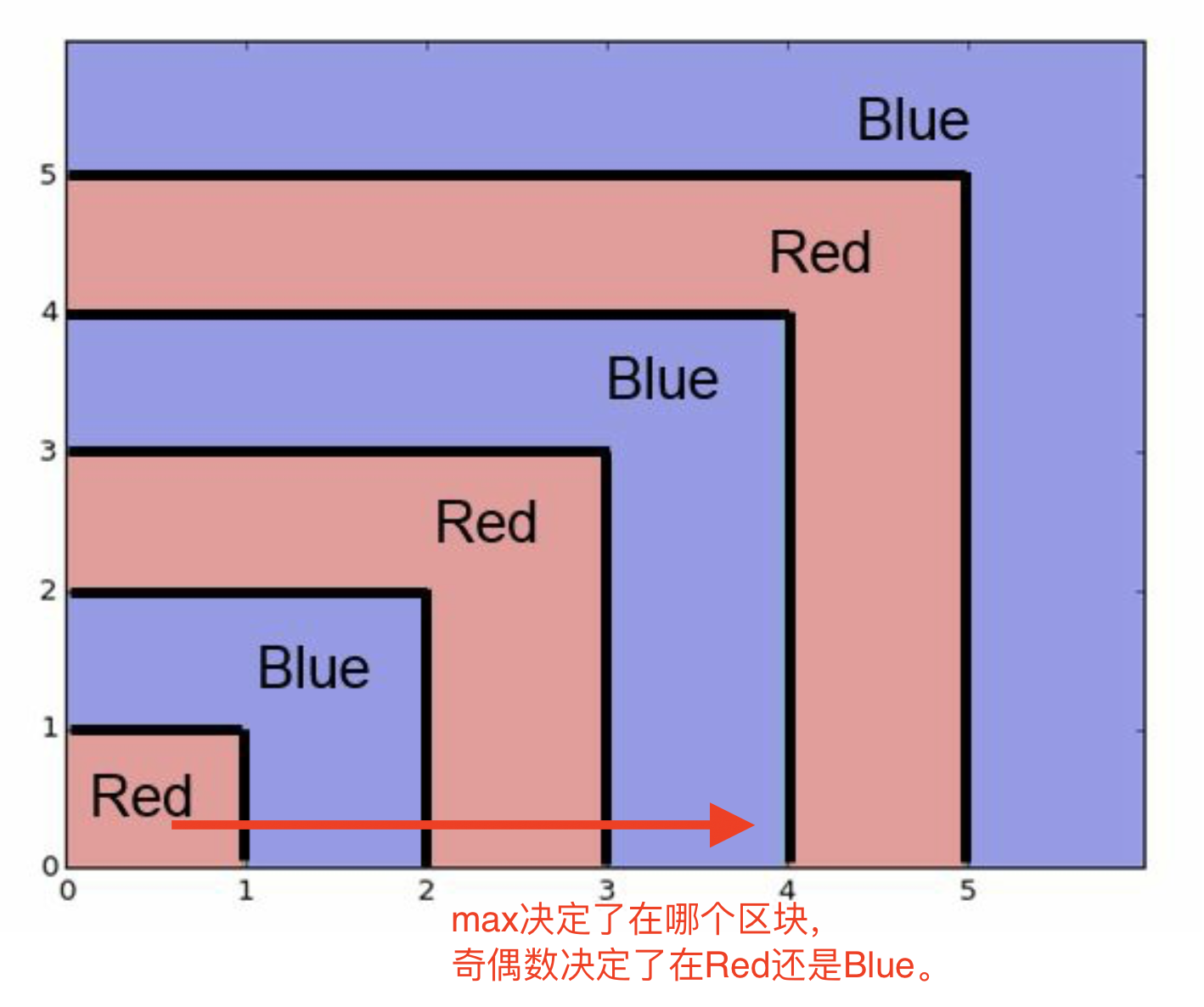
我们假设目标函数为

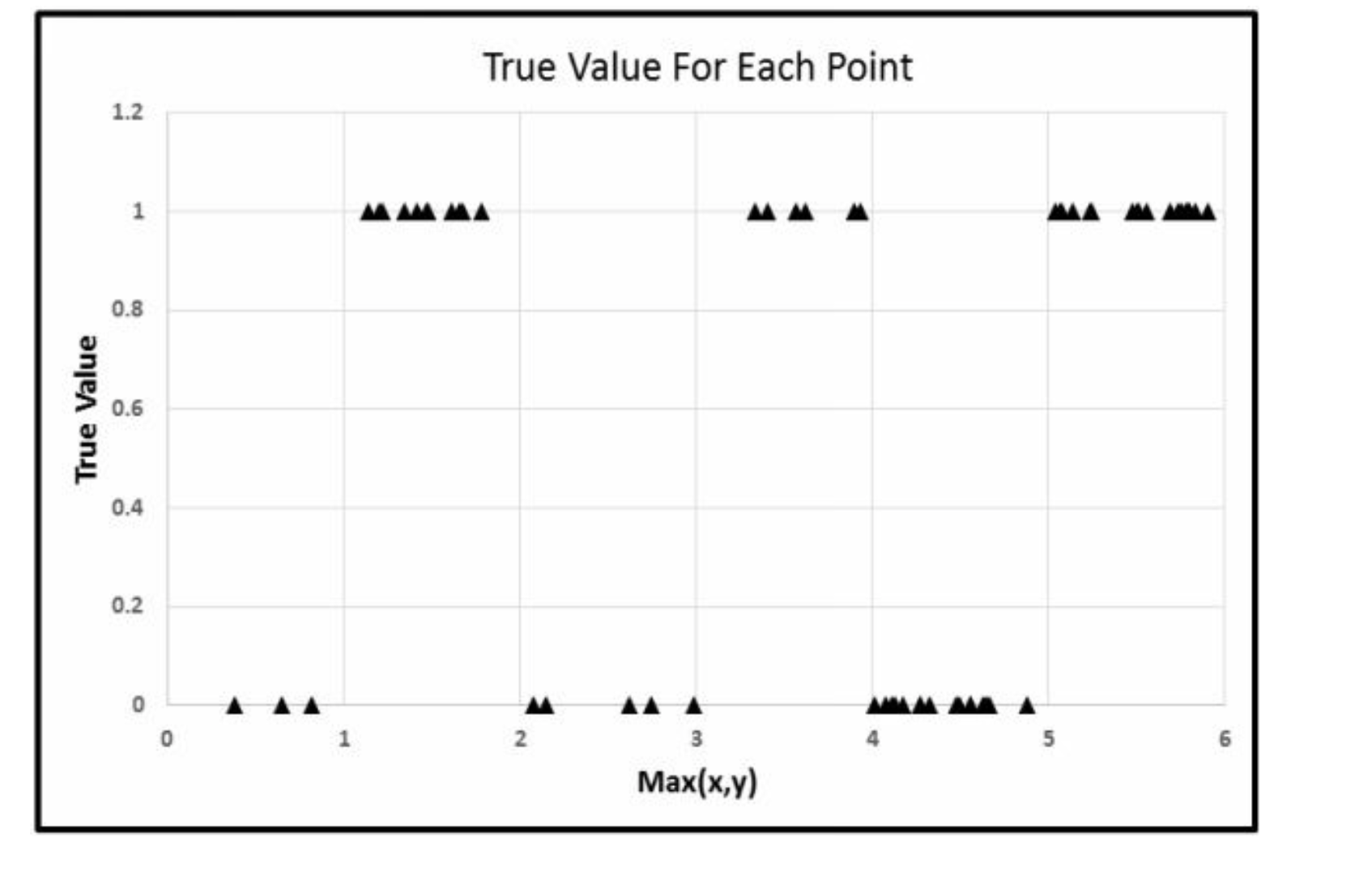
Z = int(max(X,Y)) \% 2

max决定了在哪个区块， \% 2奇偶数决定了在Red还是Blue。这里， Red=0, Blue=1。

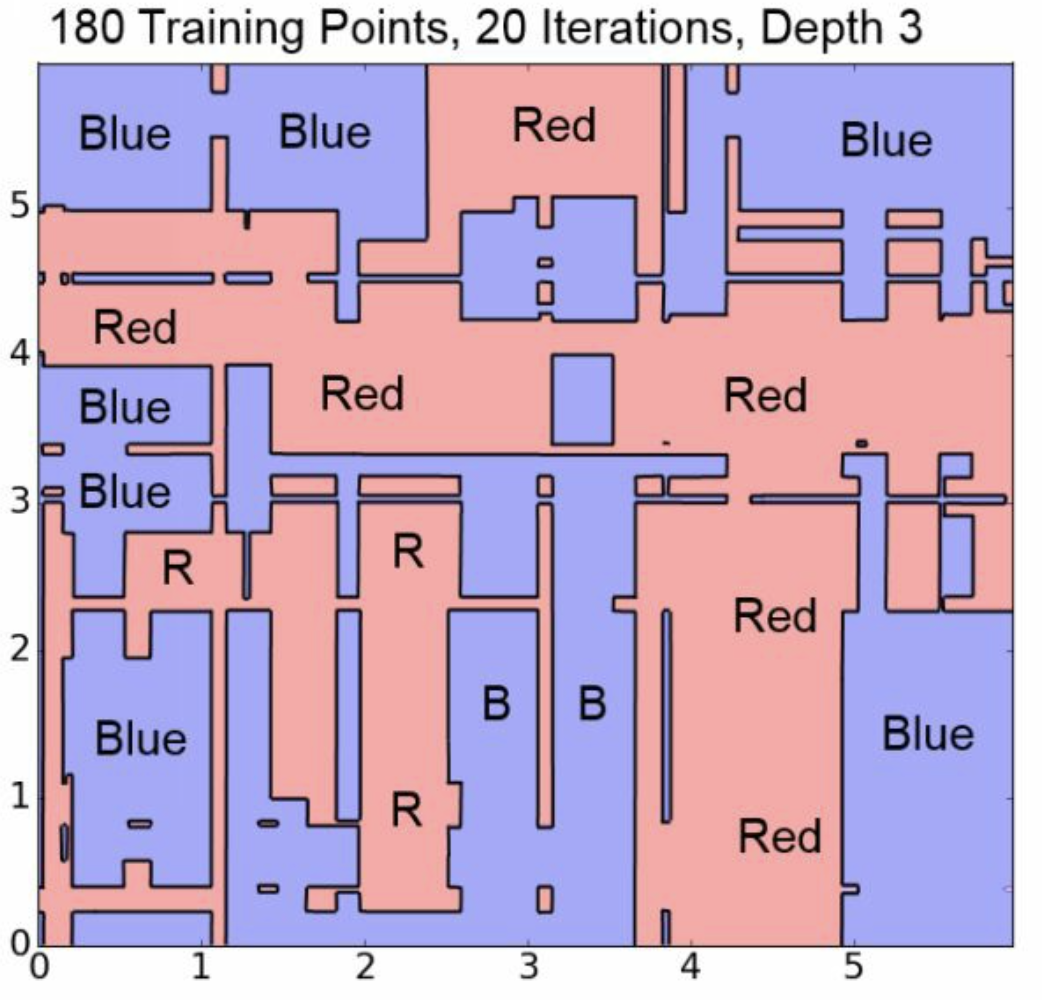
我们看到的图，其实是总体分布，实际我们是不知道的，现在我们需要用训练组去模拟出来。

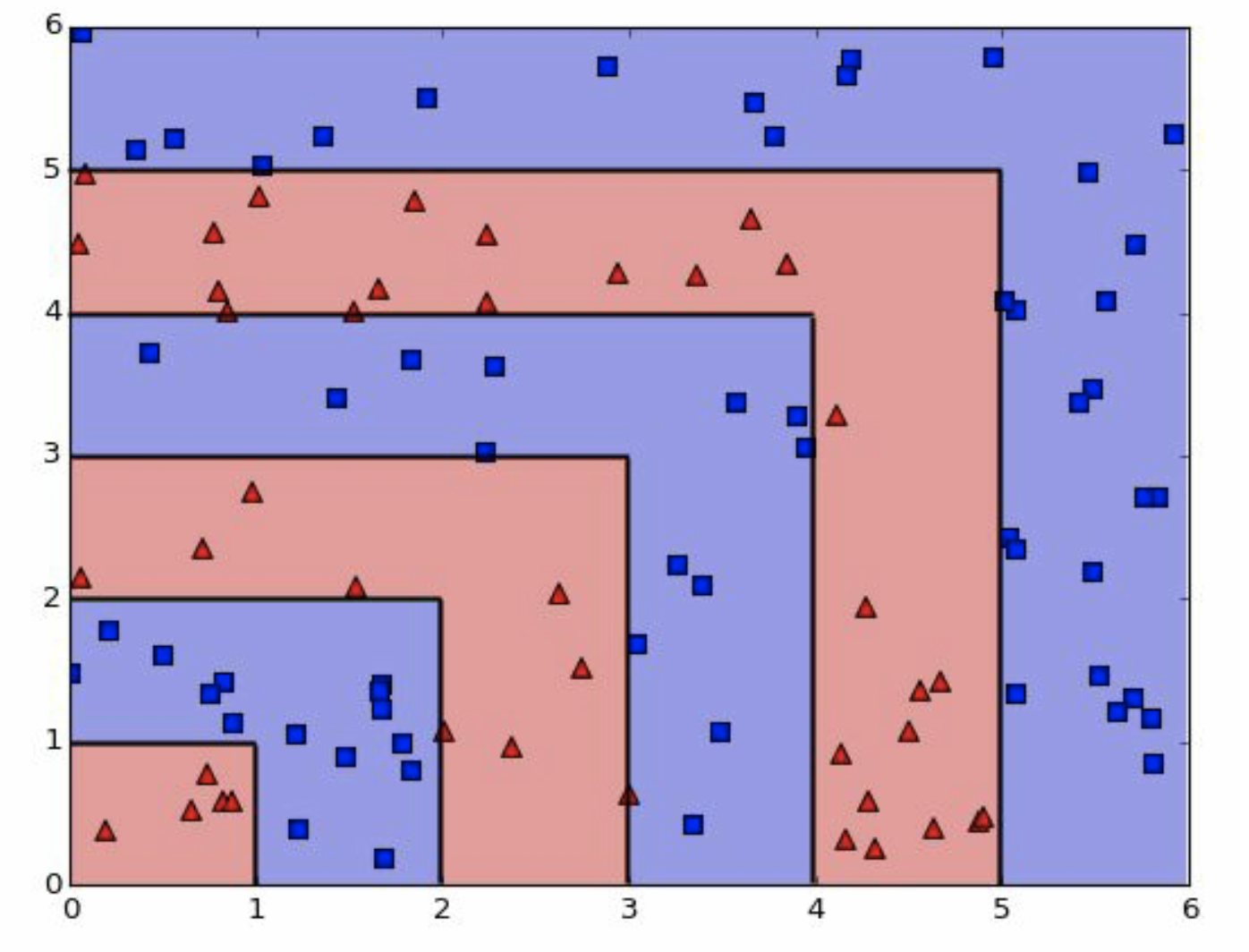
这是我们的样本，我们分个训练组出来。

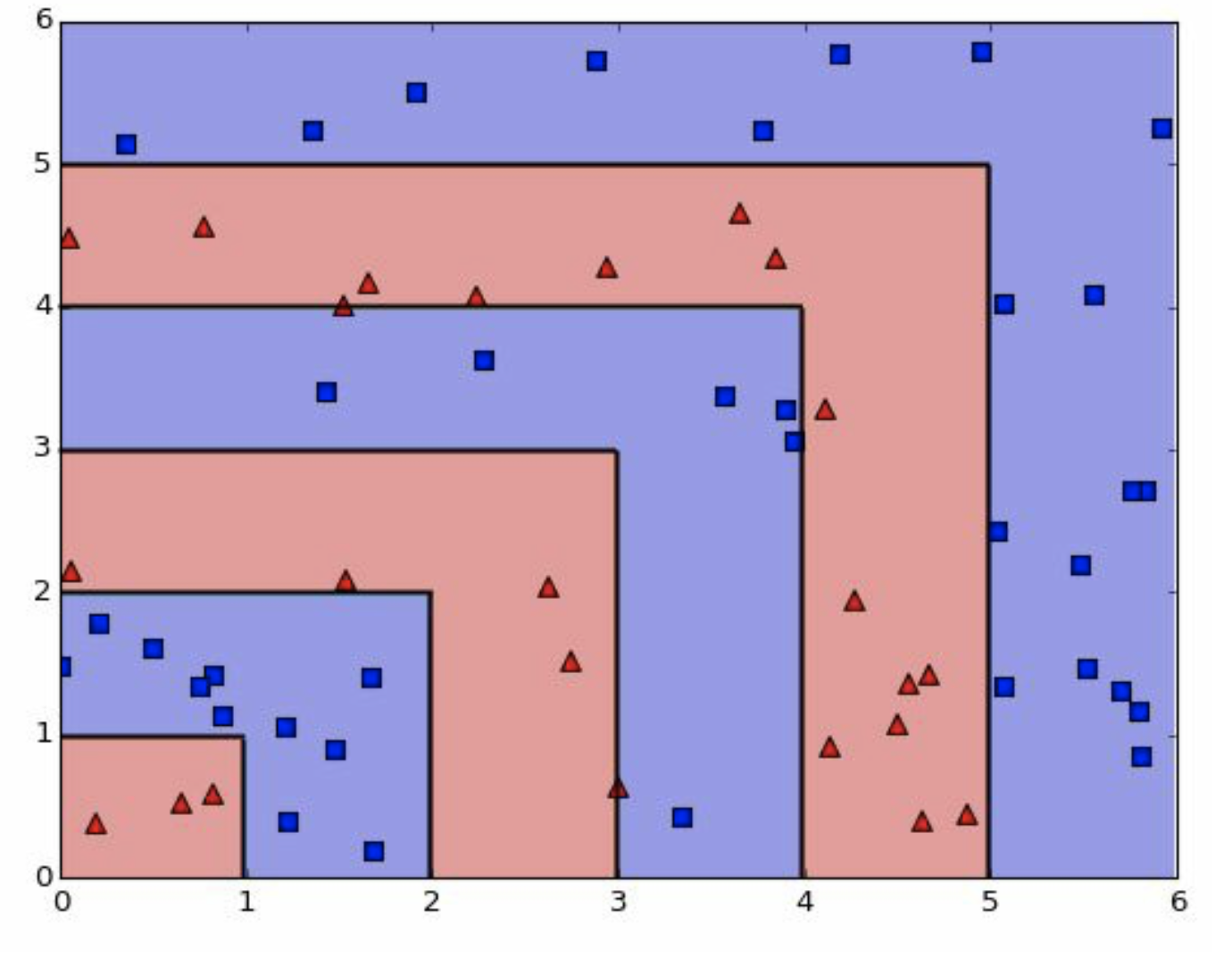
接下来我们要讨论的是 $Z \sim max (X, Y)$ 的关系，而非 $Z \sim X + Y$ 。因为现在二元问题，有点复杂，我们直接讲一元问题。但是这个max函数很好理解的，图上也标注了。并且，max(X,Y)对于每个点也是唯一的² 。

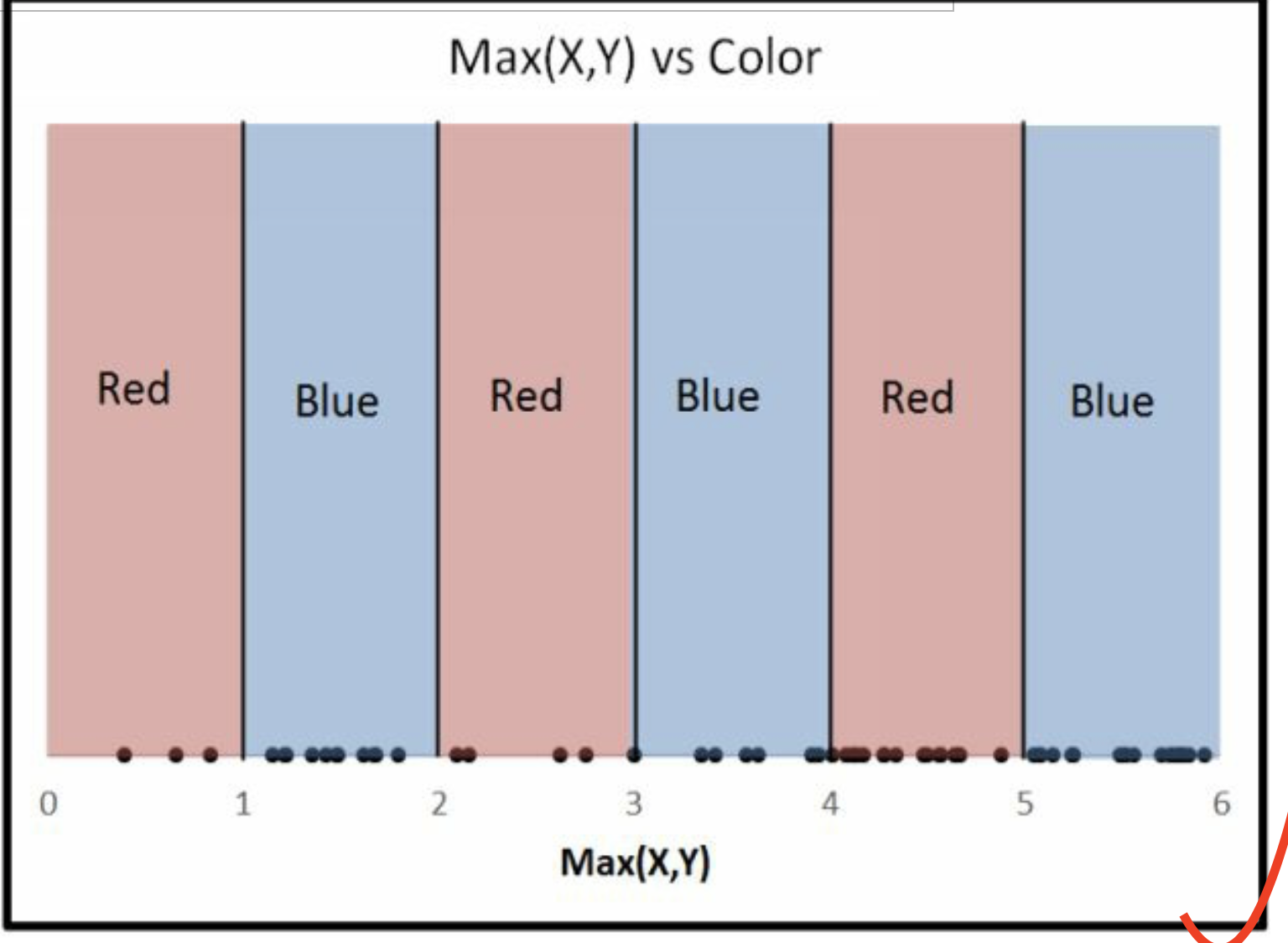
$\begin{aligned} {\hat{u}}_{0} & - & {\hat{y}}_{1} & = & {\hat{u}}_{1} \\ 0, 1 & 0.6 & - 0.6, 0.4 \end{aligned}$

${\hat{y}}_{1} = \bar{y} = 0.6$

${\hat{u}}_{1}$ 都下降了 $0.6$

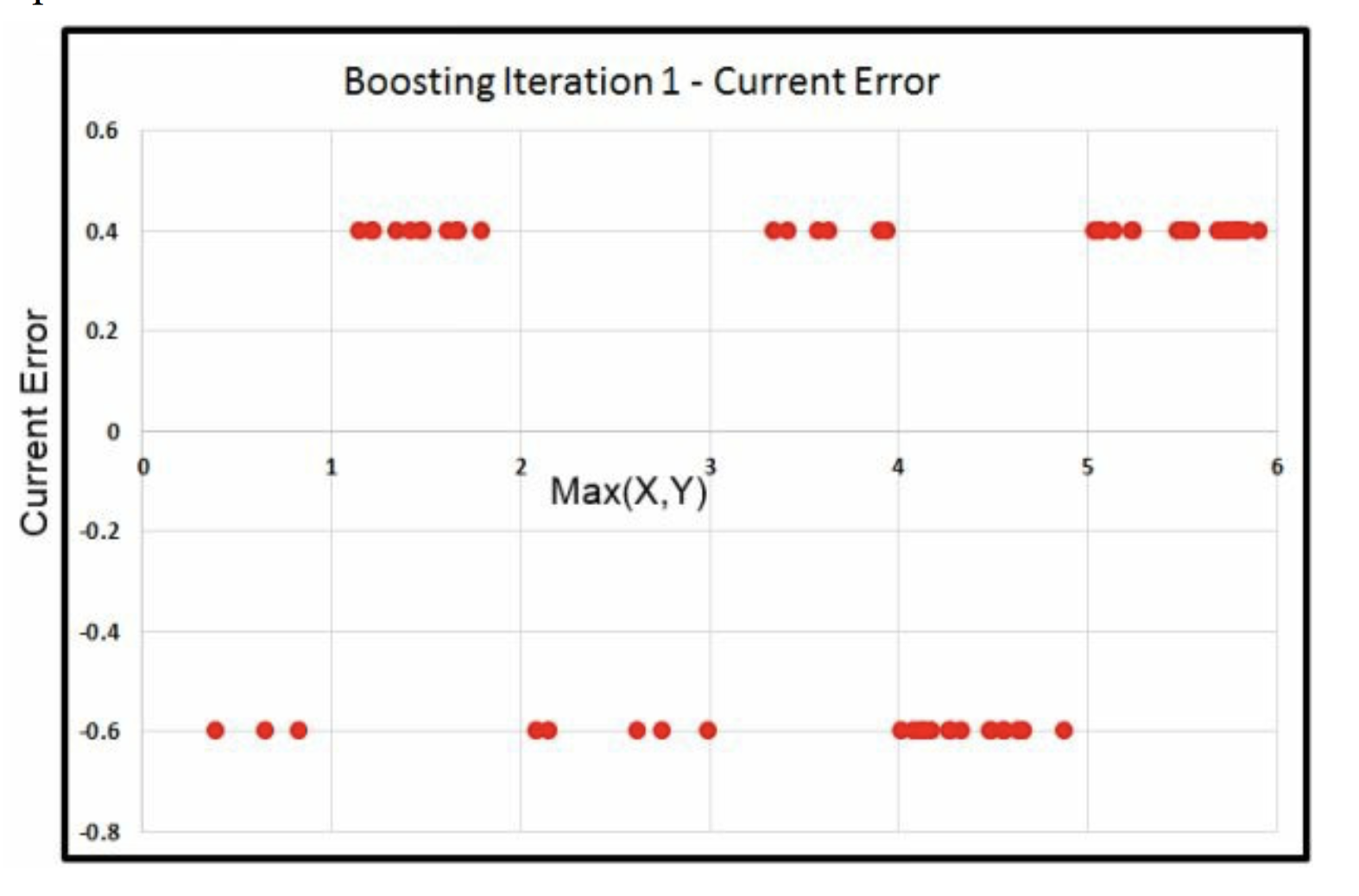
Iter1

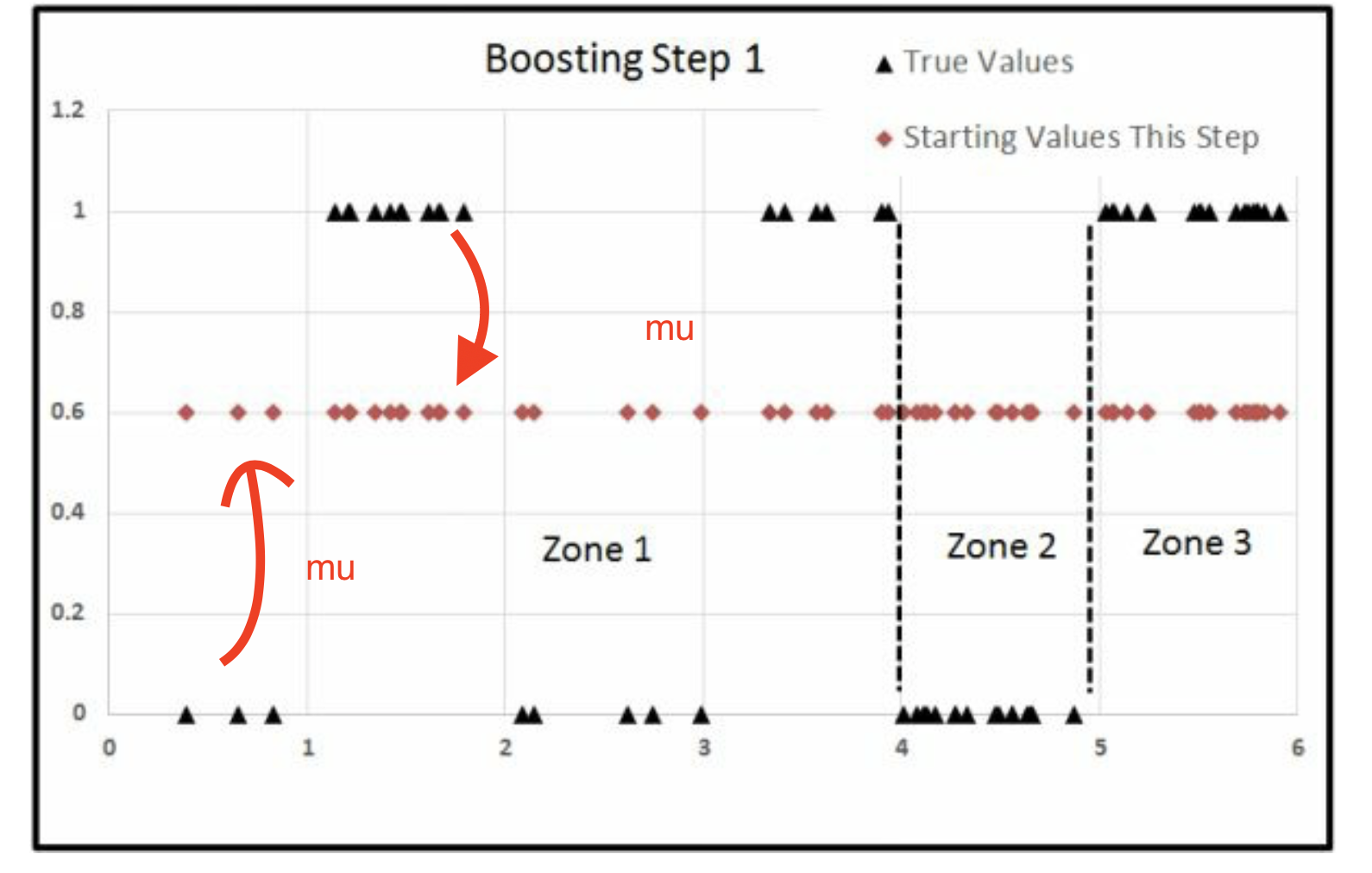
计算Zone3的变化

$\frac{\sum {\hat{u}}_{1}}{\sum {\hat{y}}_{1} (1 - {\hat{y}}_{1})} = \frac{19 \times 0.4}{19 \times 0.6 \times (1 - 0.6)} = 1.6667$

那么

$\begin{aligned} \ln (\frac{{\hat{y}}_{1}}{1 - {\hat{y}}_{1}}) & + & \frac{\sum {\hat{u}}_{1}}{\sum {\hat{y}}_{1} (1 - {\hat{y}}_{1})} & = \ln (\frac{{\hat{y}}_{2}}{1 - {\hat{y}}_{2}}) \\ \ln (\frac{0.6}{1 - 0.6}) & + & 1.6667 & = \ln (\frac{{\hat{y}}_{2}}{1 - {\hat{y}}_{2}}) \\ \to \\ {\hat{y}}_{2} = 0.8882 \end{aligned}$

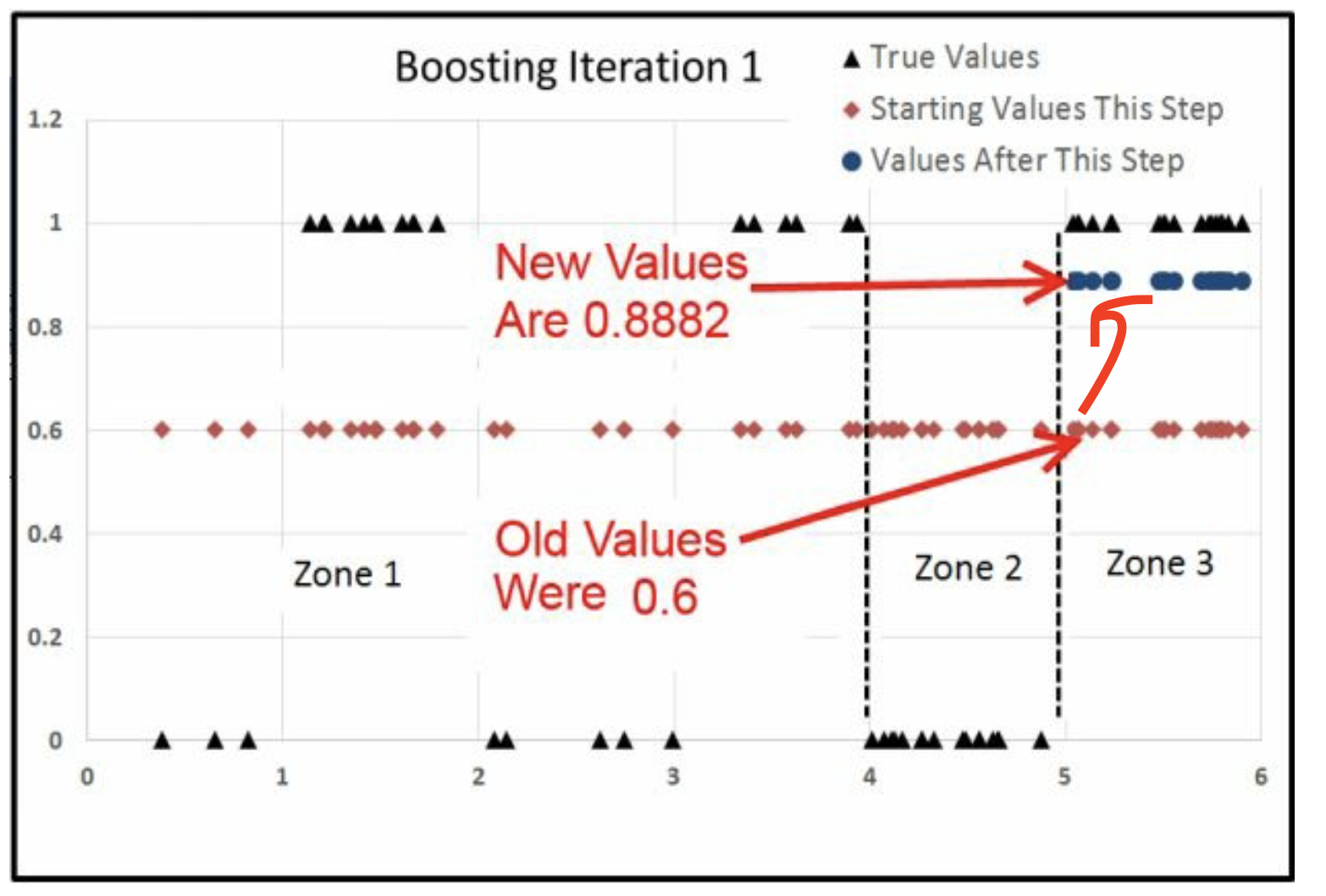
zone2

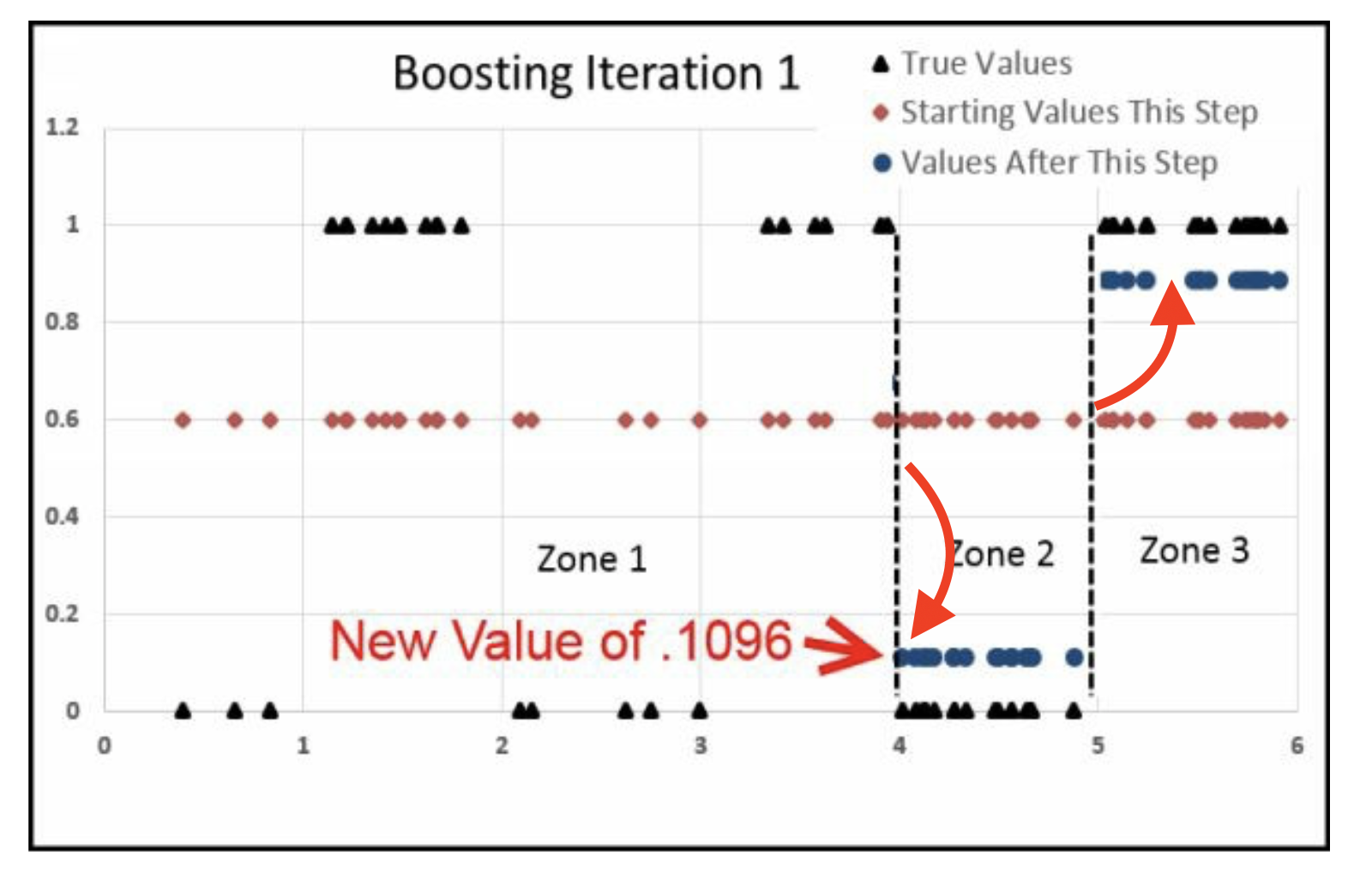
zone3

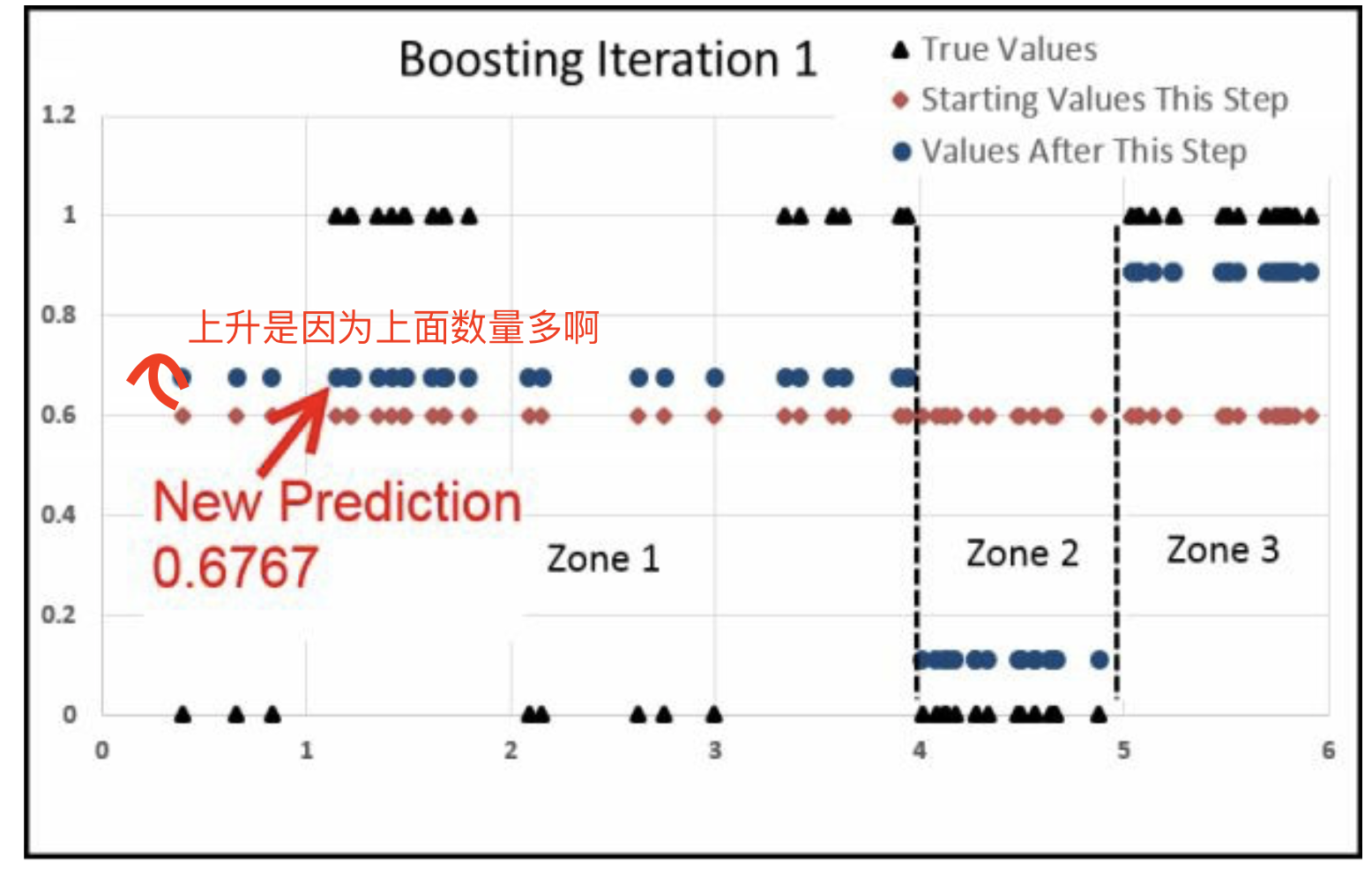
最后

zone1上升了很多
zone2下降了很多
zone3上升了一点

三刀的过程

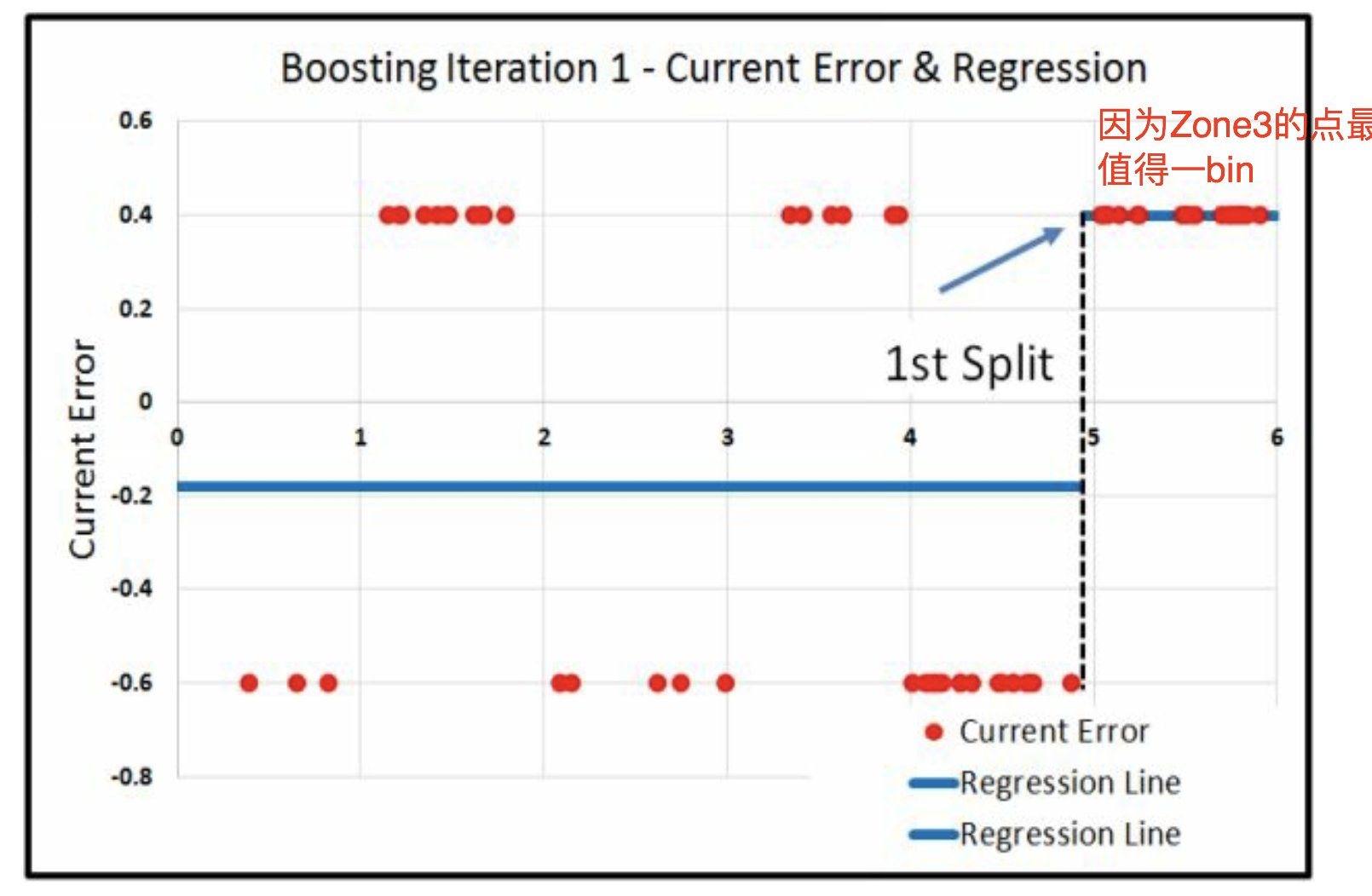
因为Zone3的点最多值得一bin

我的感觉是，因为6个组中间，最右一组的数量最多，所以先单独分出去。最右二组的数量也多，所以也单独分出去。

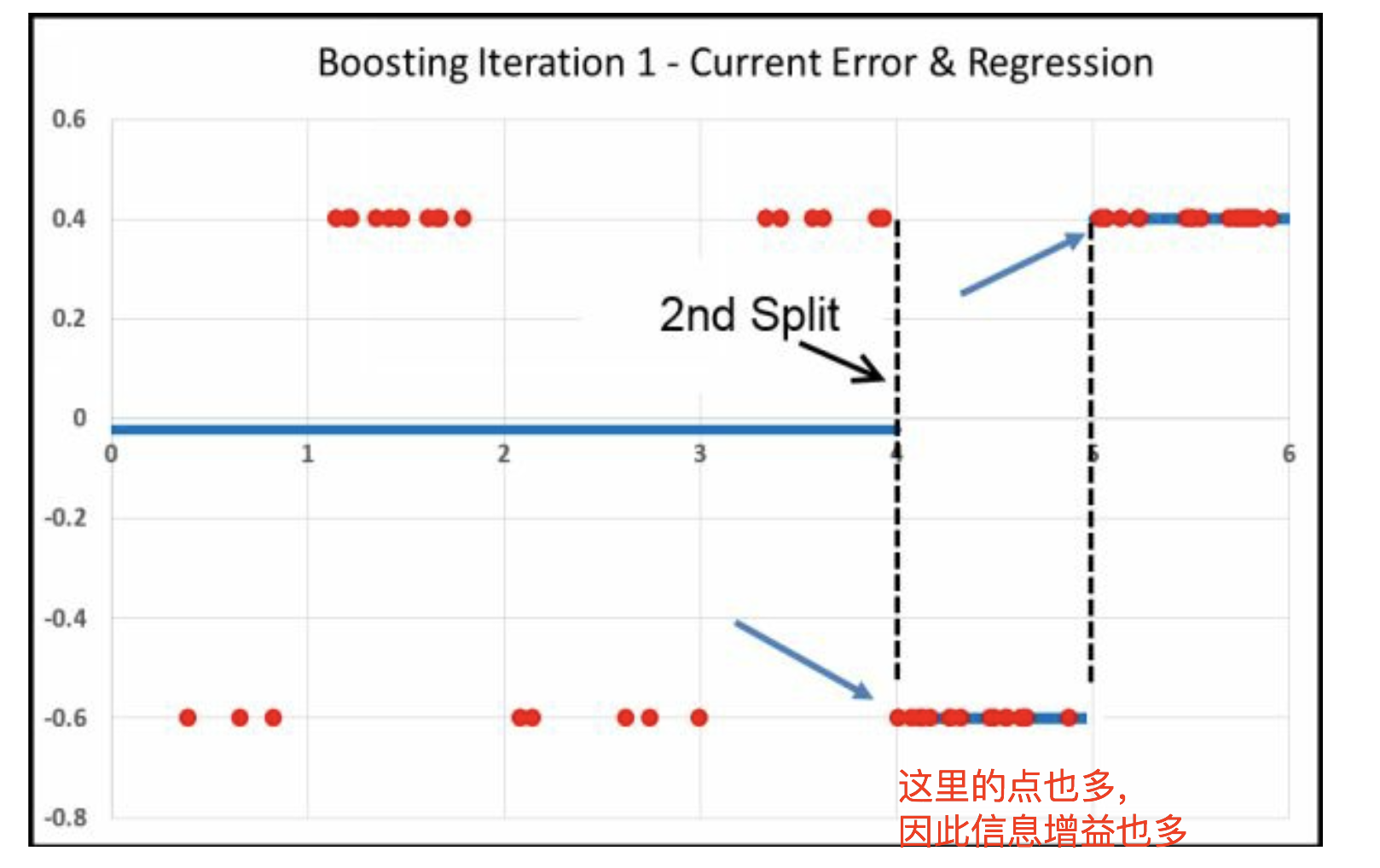
Iter2

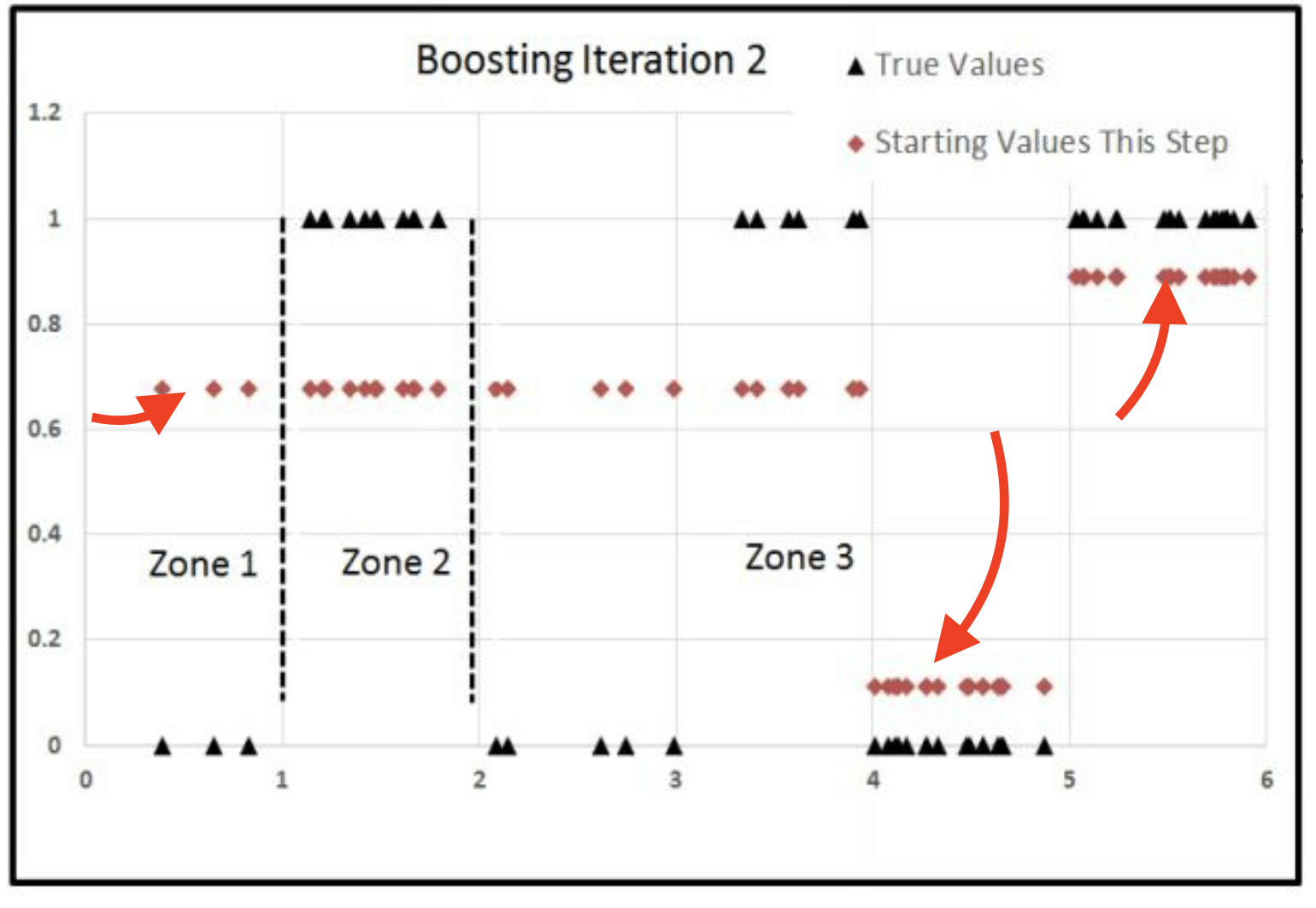
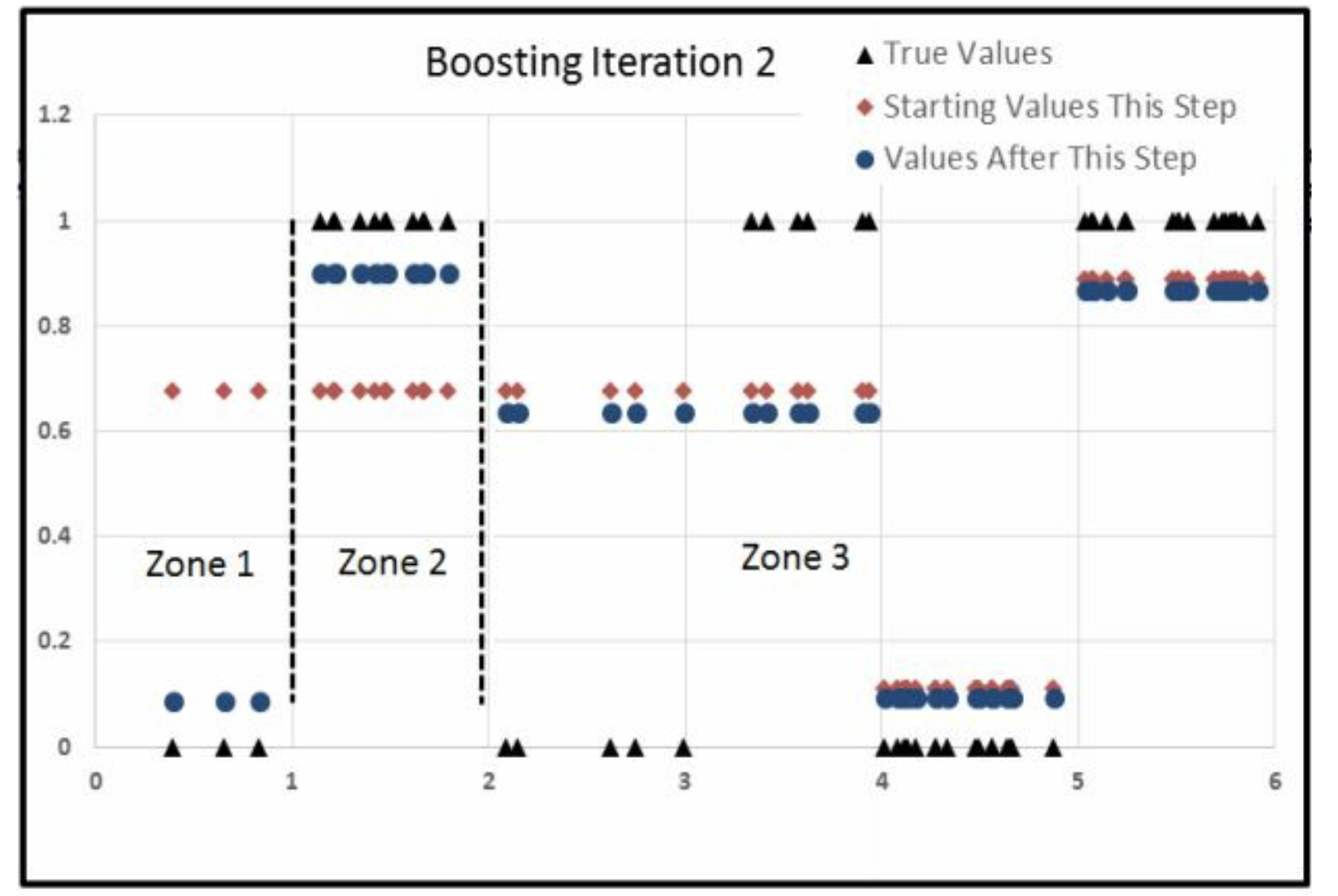
Iter3

为什么跑中间了，因为中间的Error大，其他都因为分工被针对过了，因此这些大的Error的被氛围一组，恰好在中间。因此就是先右边，再左边，最后中间。

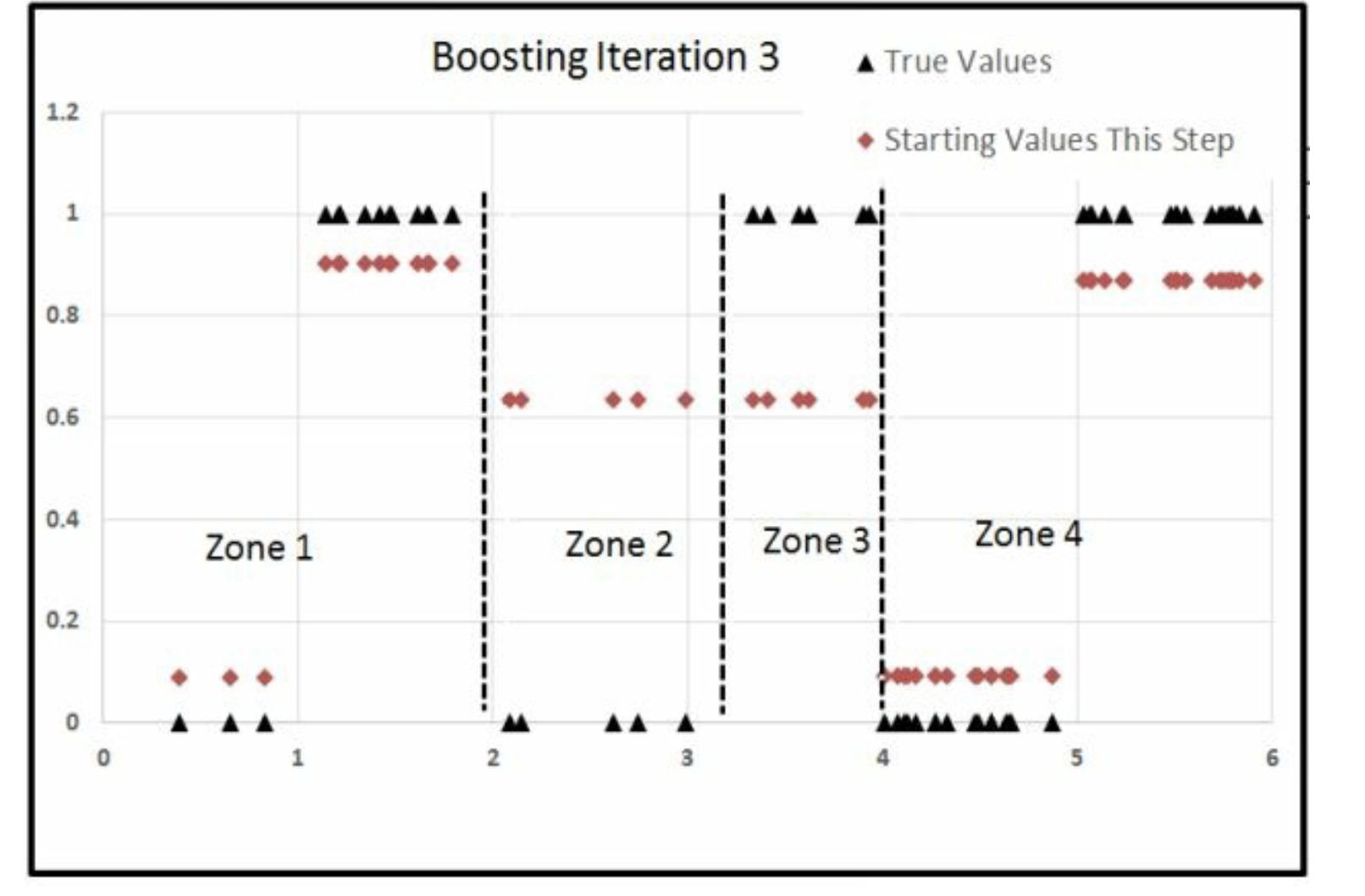
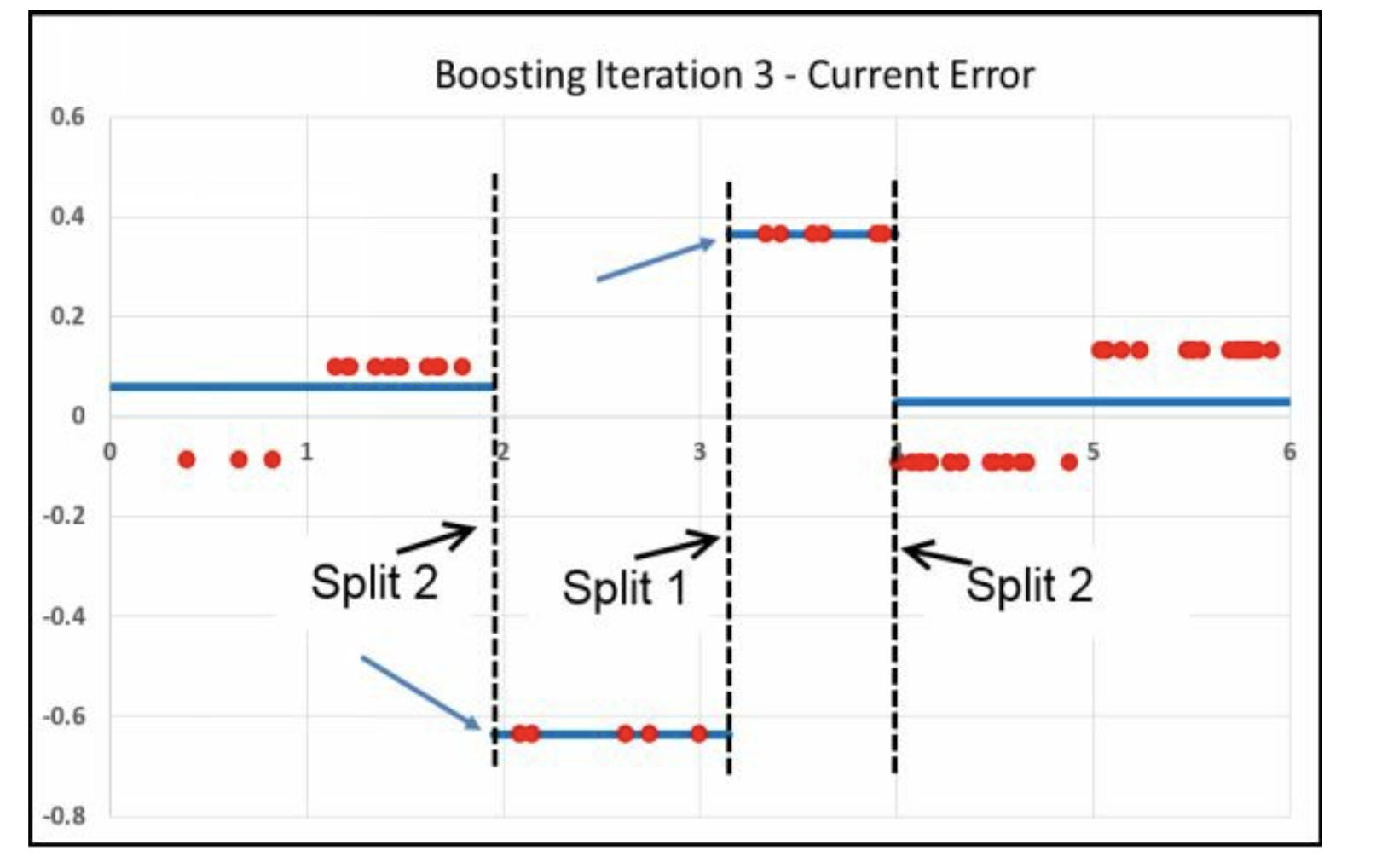
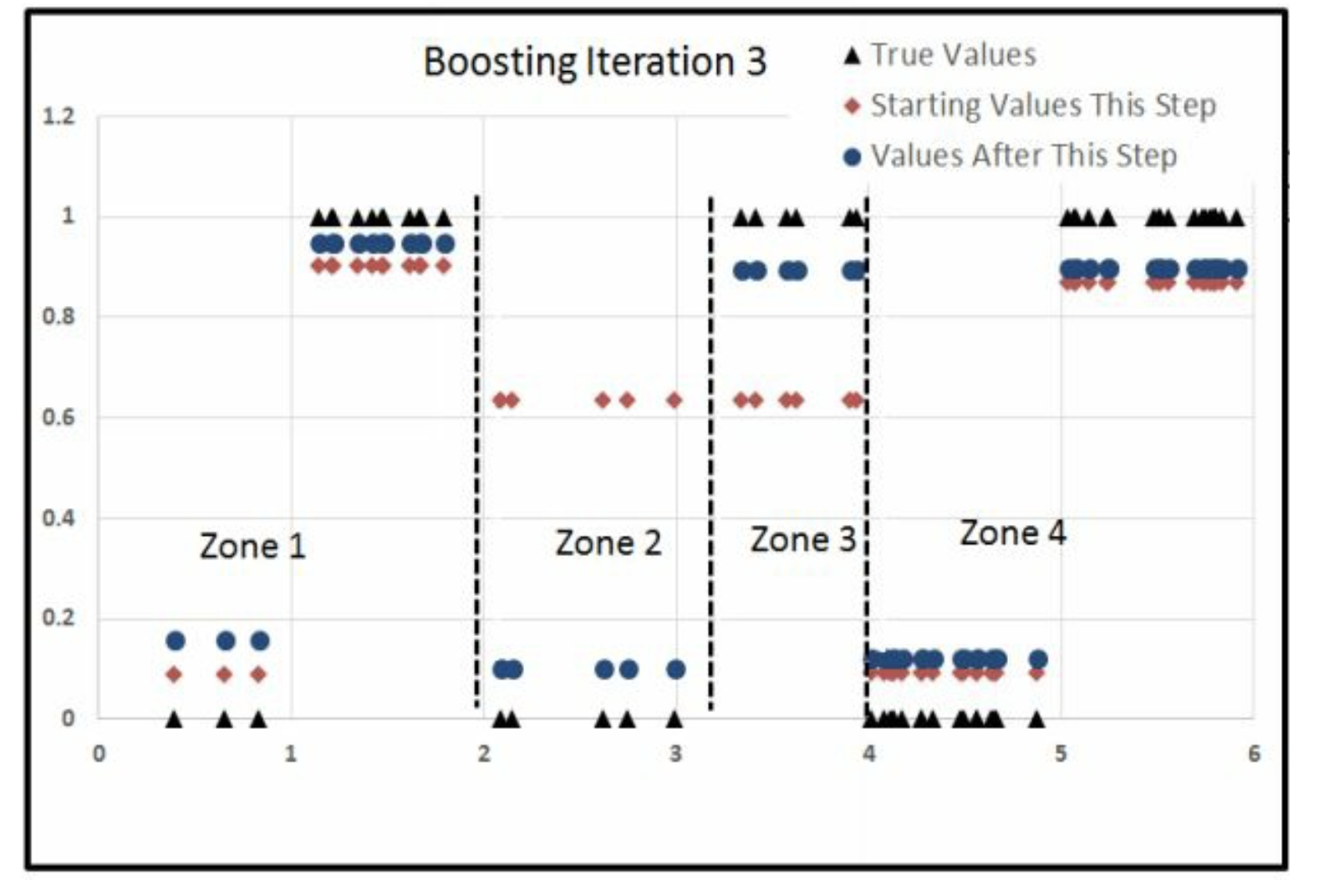
8.2 总结2

classification 涉及两个函数

logit函数

$p = \frac{1}{1 + e^{- z}}$

expit函数

$z = \ln (\frac{p}{1 - p})$

它们互为反函数

$z$ 和 $p$ 定义域不同³，

$z \in (- \infty, + \infty)$
$p \in [0, 1]$

但是正相关

$z = 0 \to y = \frac{1}{2}$
$z = - \infty \to y = 0$
$z = + \infty \to y = 1$

我们看看实际效果

$p = 0.50 \to z = 0$
$p = 0.75 \to z = + 1.09 \times 1$
$p = 0.90 \to z = + 1.09 \times 2$
$p = 0.96 \to z = + 1.09 \times 3$
$p = 0.99 \to z = + 1.09 \times 4$

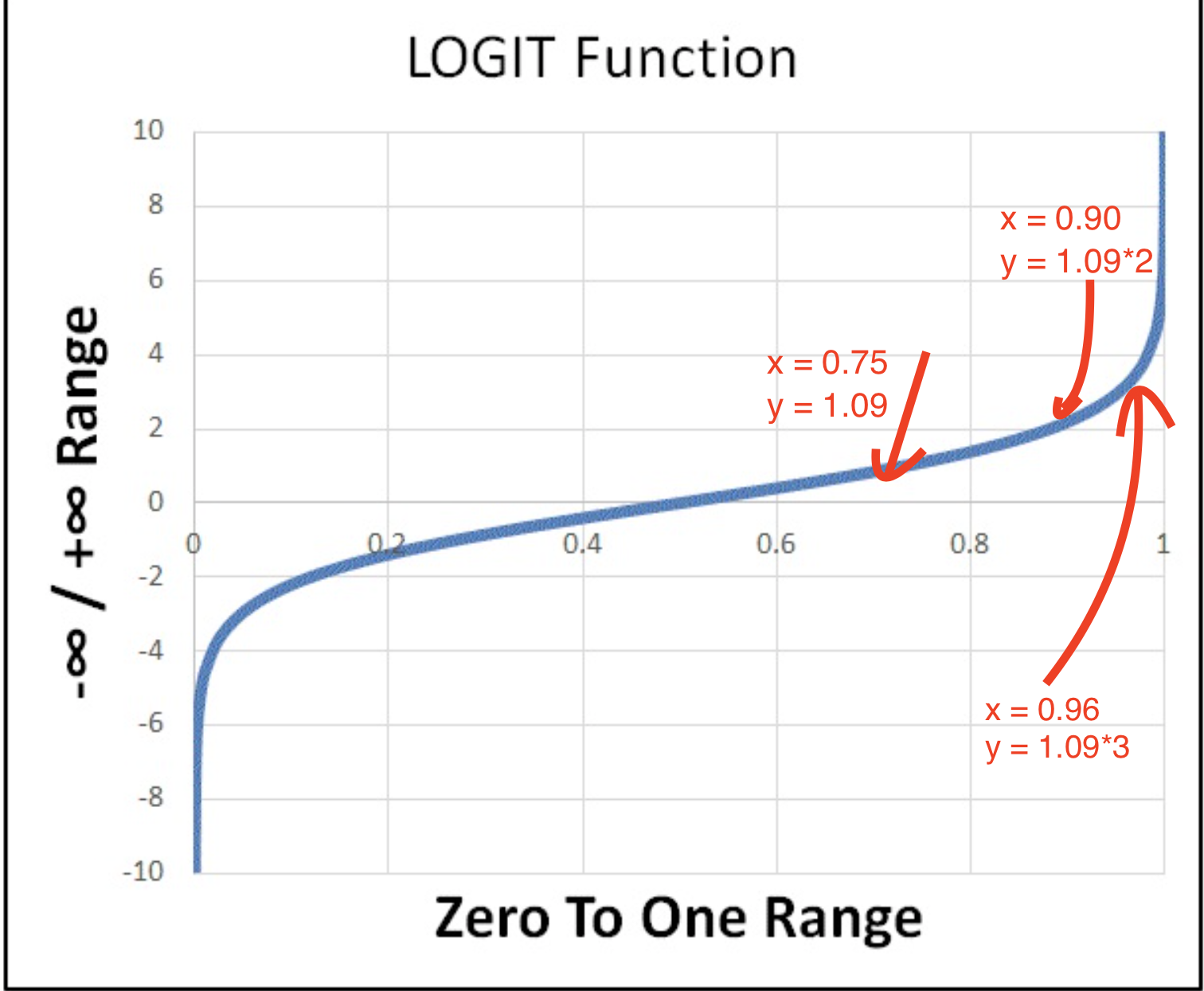
因此我们发现 $z \to p$ 是一个边际递减的过程，类似于经济学的效用函数，因此这种假设实际用的时候还是蛮bug的，因此有时候用ReLu函数，SVM常用到。

这里我们使用了depth = 2，因此最多产生4个组。但是实际上，我们想要6个组。但是depth = 2就这点能力，没办法。

Iter =1的时候，我们从右边开始切
Iter =2的时候，我们从左边开始切
Iter =3的时候，我们从中间开始切

因此这里就发生了分工。

8.3 总结3

classification相比regression，多个一个转换函数和转换函数反函数的过程。这里使用logit和expit函数。

当我们拿到数据的时候，我们假设 $y = {\hat{u}}_{0}$ $\bar{y} = {\hat{y}}_{1}$

因此得到

${\hat{u}}_{1} = {\hat{u}}_{0} - {\hat{y}}_{1}$

因为每个点的 ${\hat{u}}_{1}$ 都不同，我们根据 ${\hat{u}}_{1}$ 的 __相似程度__进行分刀。对分刀的各个组，我们计算

$\frac{\sum {\hat{u}}_{1}}{\sum {\hat{y}}_{1} (1 - {\hat{y}}_{1})} | g r o u p = j$

我们注意分母恒大于0，因此该公式的正负受到 $\sum {\hat{u}}_{1}$ 决定。我们知道如果该公式中大部分 ${\hat{u}}_{1} > 0$ ，那么就是 $+$ ，反之 $-$ 。 ${\hat{u}}_{1} > 0 \to {\hat{u}}_{0} (= 1) > {\hat{y}}_{1}$ ，因此 ${\hat{y}}_{1}$ 估计太小，需要增加。

$\ln (\frac{{\hat{y}}_{1}}{1 - {\hat{y}}_{1}}) + \frac{\sum {\hat{u}}_{1}}{\sum {\hat{y}}_{1} (1 - {\hat{y}}_{1})} = \ln (\frac{{\hat{y}}_{2}}{1 - {\hat{y}}_{2}})$

因此 ${\hat{y}}_{1} ↑\to {\hat{y}}_{2}$

同理

$\ln (\frac{{\hat{y}}_{i}}{1 - {\hat{y}}_{i}}) + \frac{\sum {\hat{u}}_{i}}{\sum {\hat{y}}_{i} (1 - {\hat{y}}_{i})} = \ln (\frac{{\hat{y}}_{i + 1}}{1 - {\hat{y}}_{i + 1}})$

8.4 总结4

以上特征变量只有一个，当特征变量超过一个时，其实也是类似的，这里就不叙述了。

9 多分类的理解

9.1 总结1

假设我们有一个训练组，有三类。样本占比为 ${z_{1}, z_{2}, z_{3}}$ 。显然 $\sum (z_{1}, z_{2}, z_{3}) = 1$ ， $z_{1}, z_{2}, z_{3} \in [0, 1]$ 。

用one vs. rest approach

Iter1

${z_{1}, z_{2}, z_{3}}$ $\overset{{\hat{y}}_{1}^{1} = \frac{e^{z_{1}}}{e^{z_{1}} + e^{z_{2}} + e^{z_{3}}}}{\to}$ ${\hat{y}}_{1}^{1}$ $\overset{{\hat{u}}_{0} - {\hat{y}}_{1} = {\hat{u}}_{1}}{\to}$ ${\hat{u}}_{1}^{1}$ $\overset{相似的 u_{1}^{1} 切 b i n}{\to}$ 计算 $\frac{\sum {\hat{u}}_{1}^{1}}{\sum {\hat{y}}_{1}^{1} (1 - {\hat{y}}_{1}^{1})} \cdot \frac{n - 1}{n}$ $\overset{z_{1} := Δ + z_{1}}{\to}$ 更新 $z_{1}$

然后，完成了分类1的Iter1，把结果应用到分类2的Iter1⁴，产生更新 $z_{2}$ 后，把结果应用到分类3的Iter1。

这样完成了第一次迭代。

其中， ${\hat{y}}_{1}^{1}$ 表示类别1的第一个预测值。

9.2 总结2

因此，如果我们迭代10次，如果多分类为3个，那么一次要三次决策树，一共为 $3 \times 10$ 次决策树。因此多分类比二分类慢。

这是流程图。

一般情况下，更新的 $z_{i}$ 要比第二大的 $z_{i}$ 大6 unit，才能说，这个分的好了。

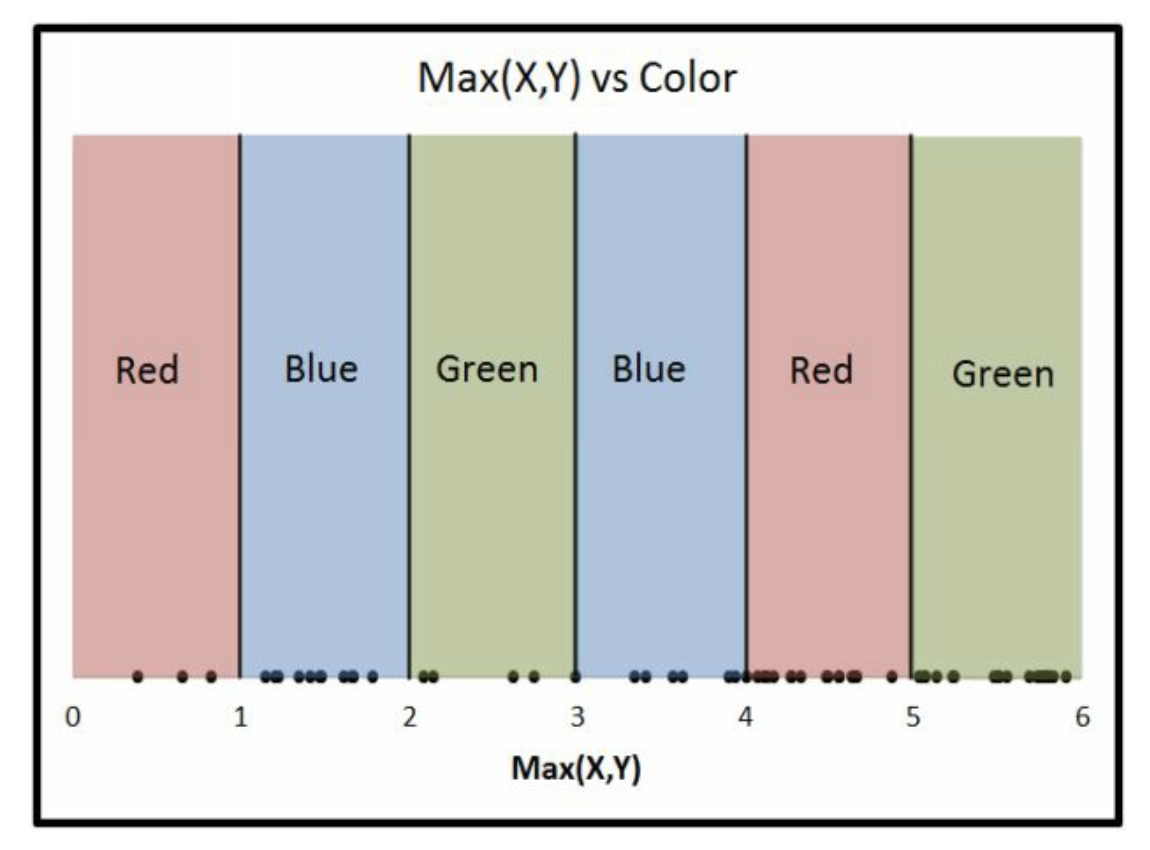
总体分布

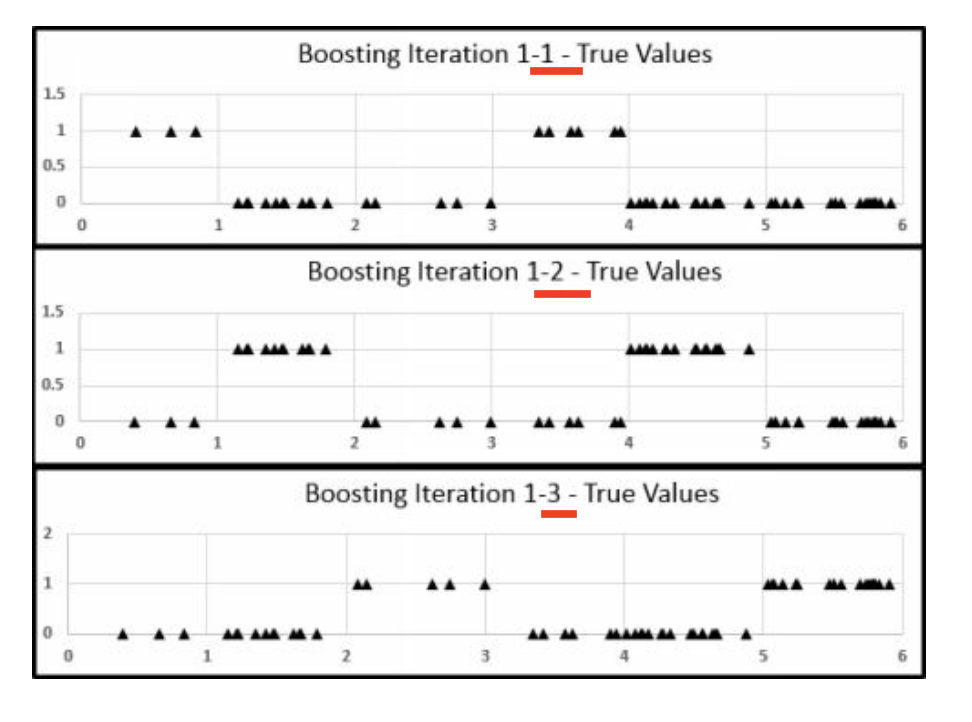
第一次迭代中，三个分类，在one vs. rest 的情况下的表现。

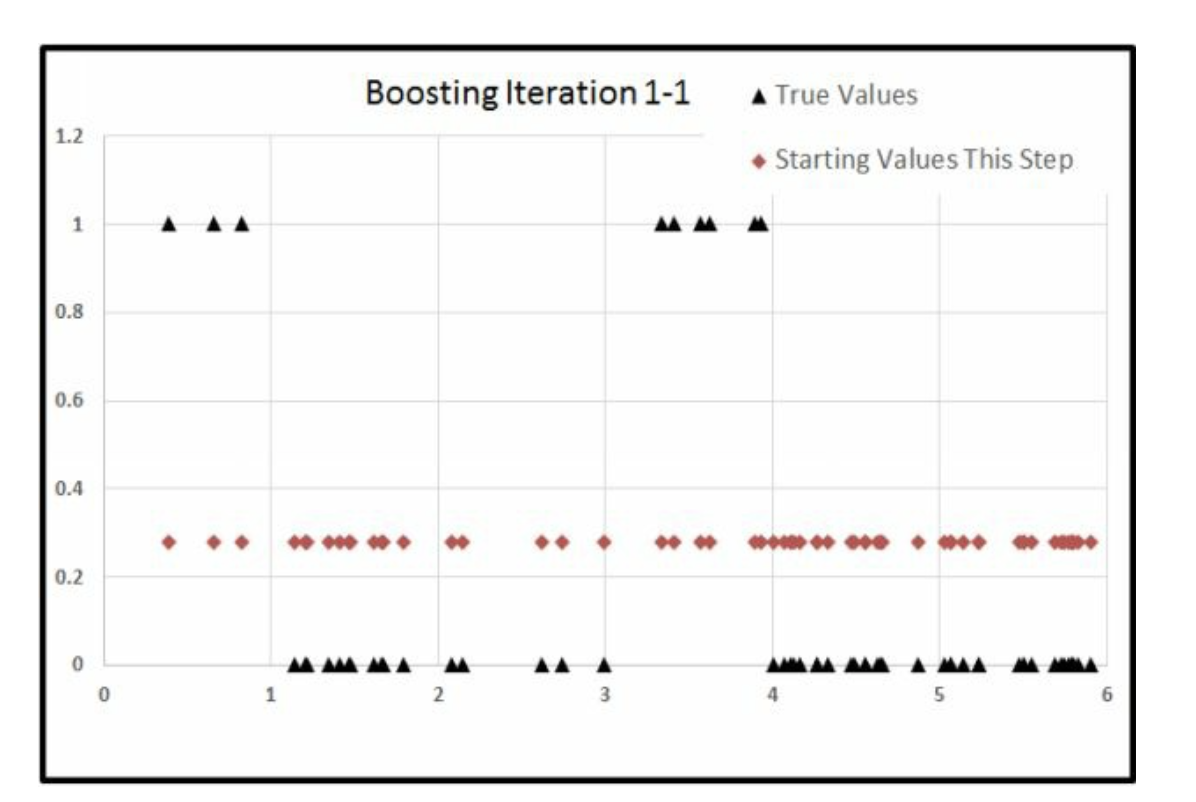
先考虑分类1，

${\hat{y}}_{1}^{1} = \frac{e^{z_{1}}}{e^{z_{1}} + e^{z_{2}} + e^{z_{3}}}$

这个是估计值。

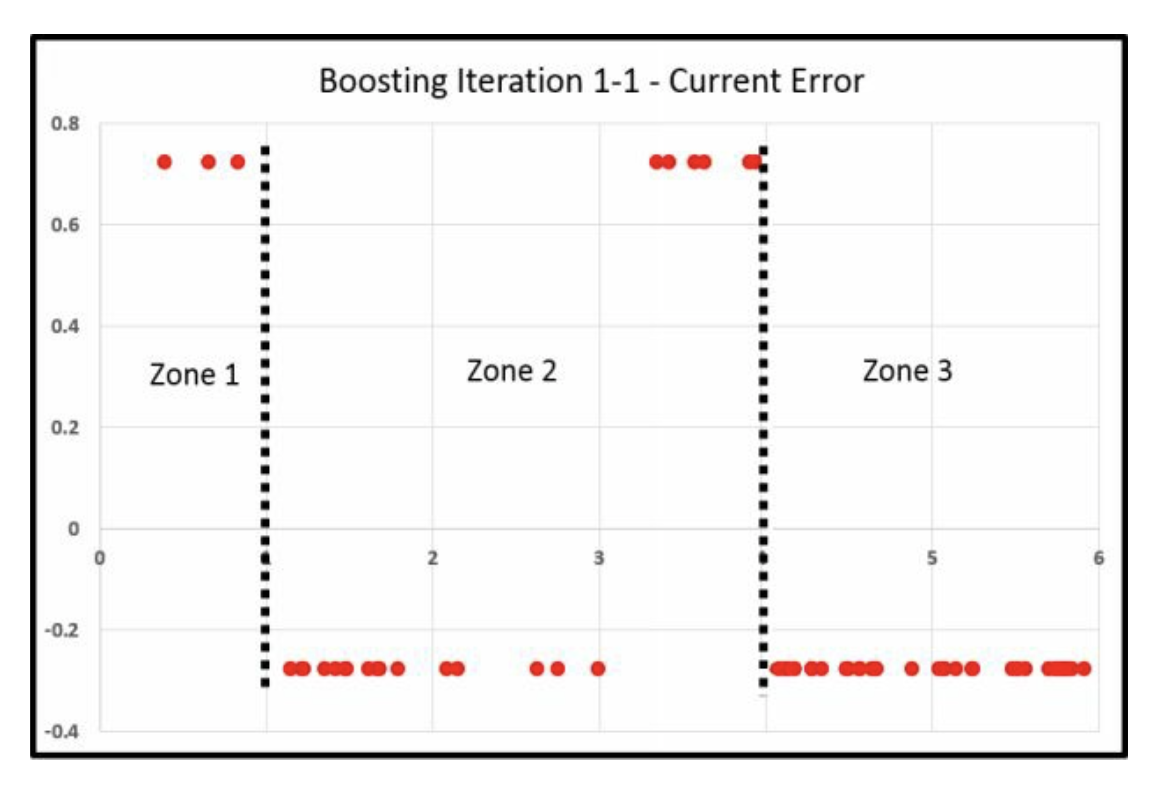
这个是第一次迭代中分类1 的分刀表现。

g1	g2	g3	ori
2.573	0.142	-0.77	0.15
0.450	0.450	0.45	0.45
0.400	0.400	0.40	0.40

g1	g2	g3	ori
0.8106962	0.2735948	0.1314202	0.2751876
0.0970177	0.3722808	0.4451449	0.3714645
0.0922861	0.3541244	0.4234349	0.3533479

注意一个是 $z$ 的区间，一个是 $\hat{y}$ 的区间。我们发现，$

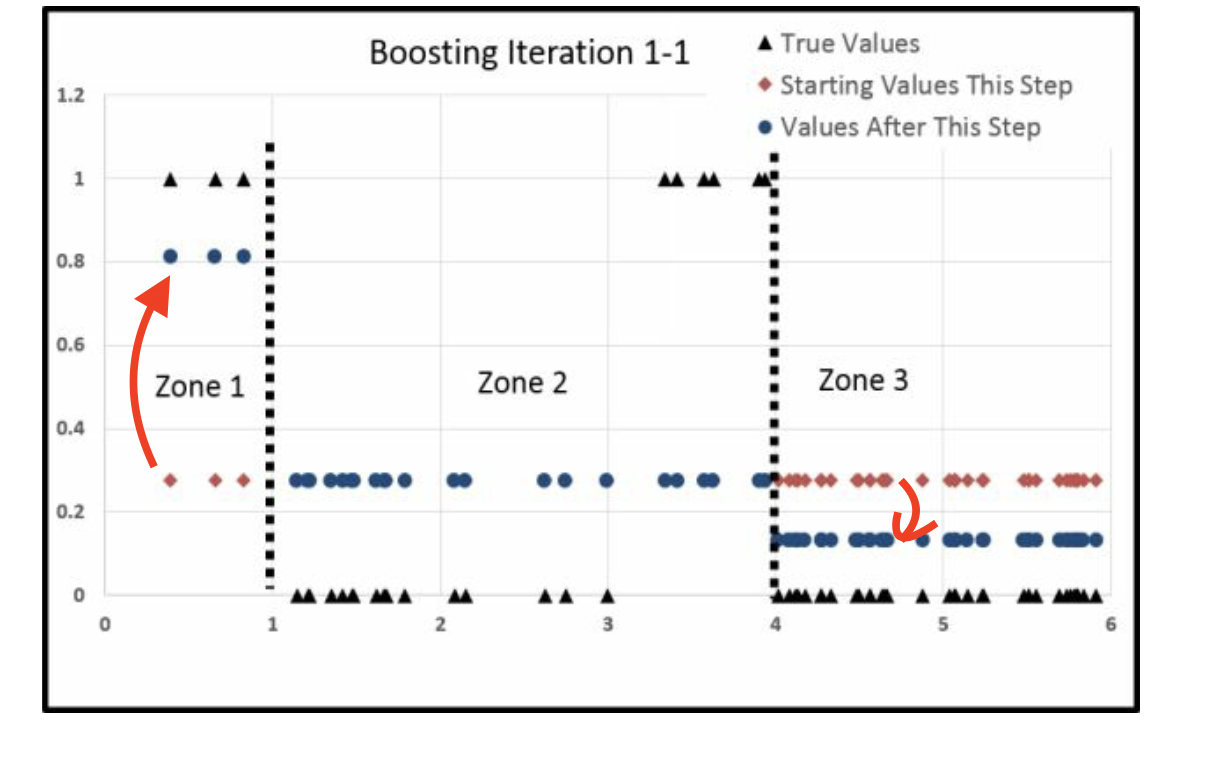
针对于第一次迭代完，分类1的新 $\hat{y}$ 的情况，如图。

再考虑分类2，

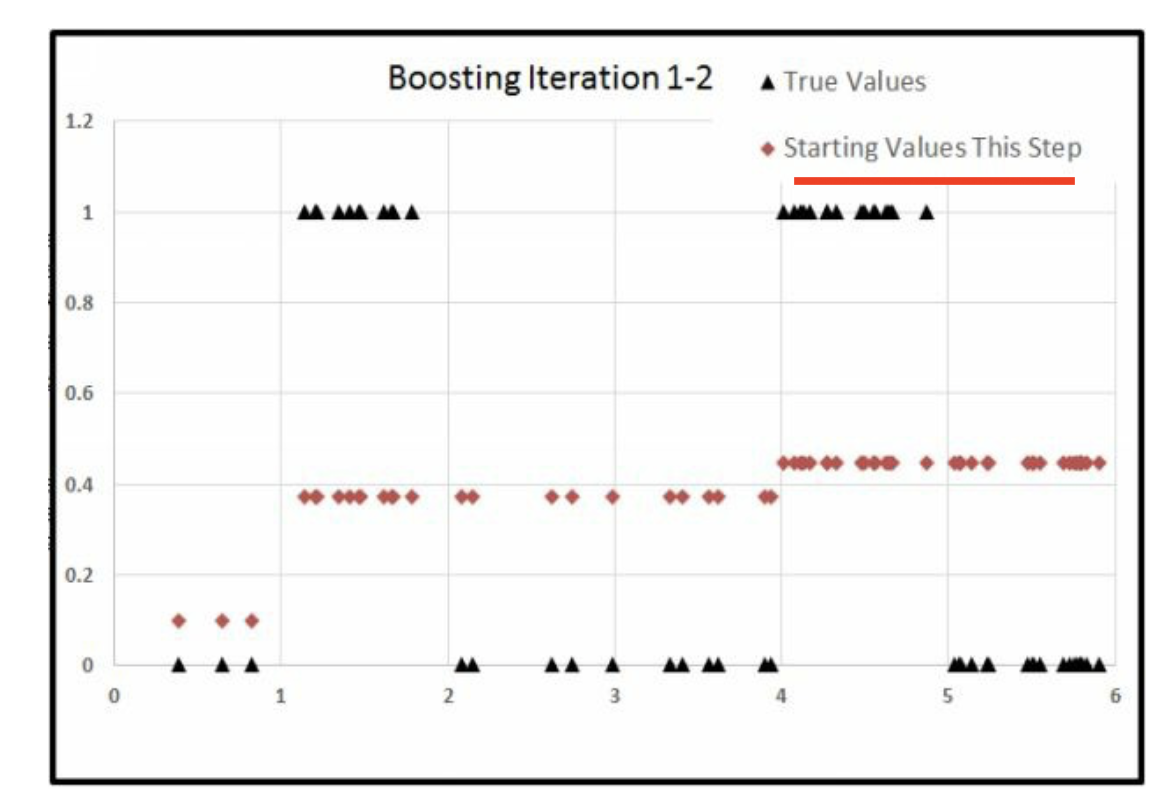
$y_{1}^{2}$ 因为 $z_{1}$ 的更新也发生了改变，但是是好的，你看图。

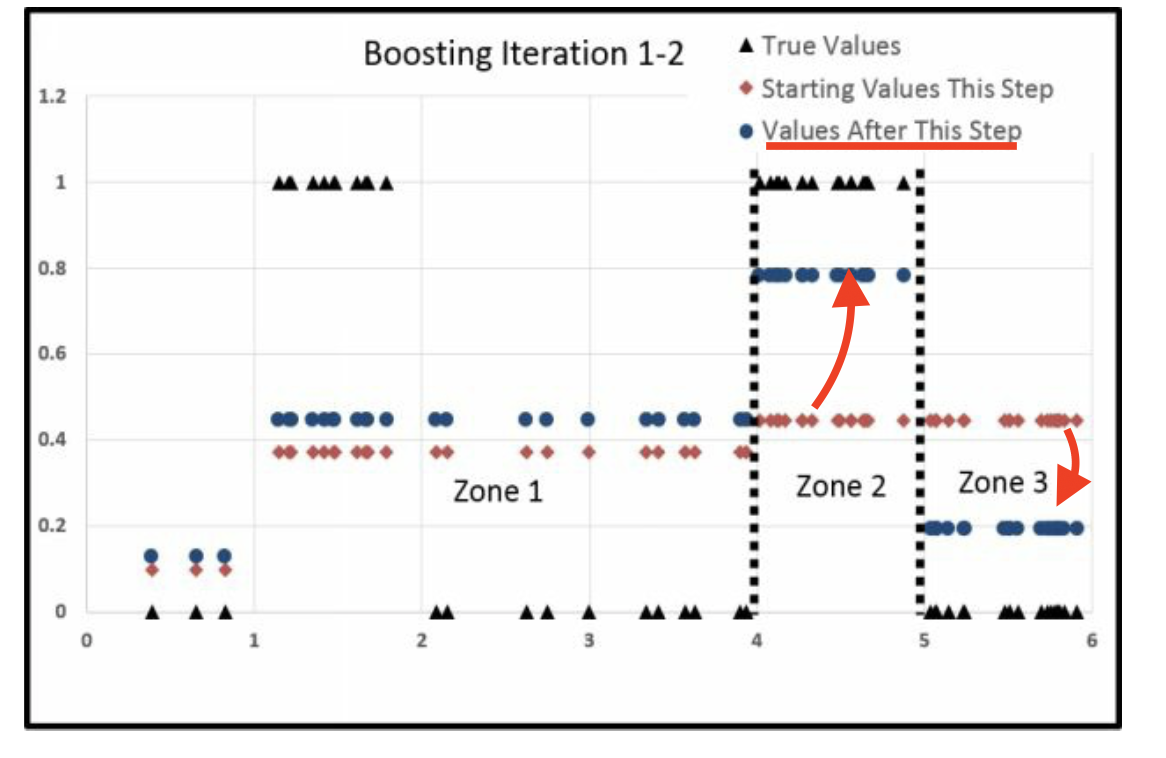
迭代完的情况。

再考虑分类3，同样， $y_{1}^{3}$ 因为 $z_{1} 和 z_{2}$ 的更新也发生了改变，但是是好的，你看图。

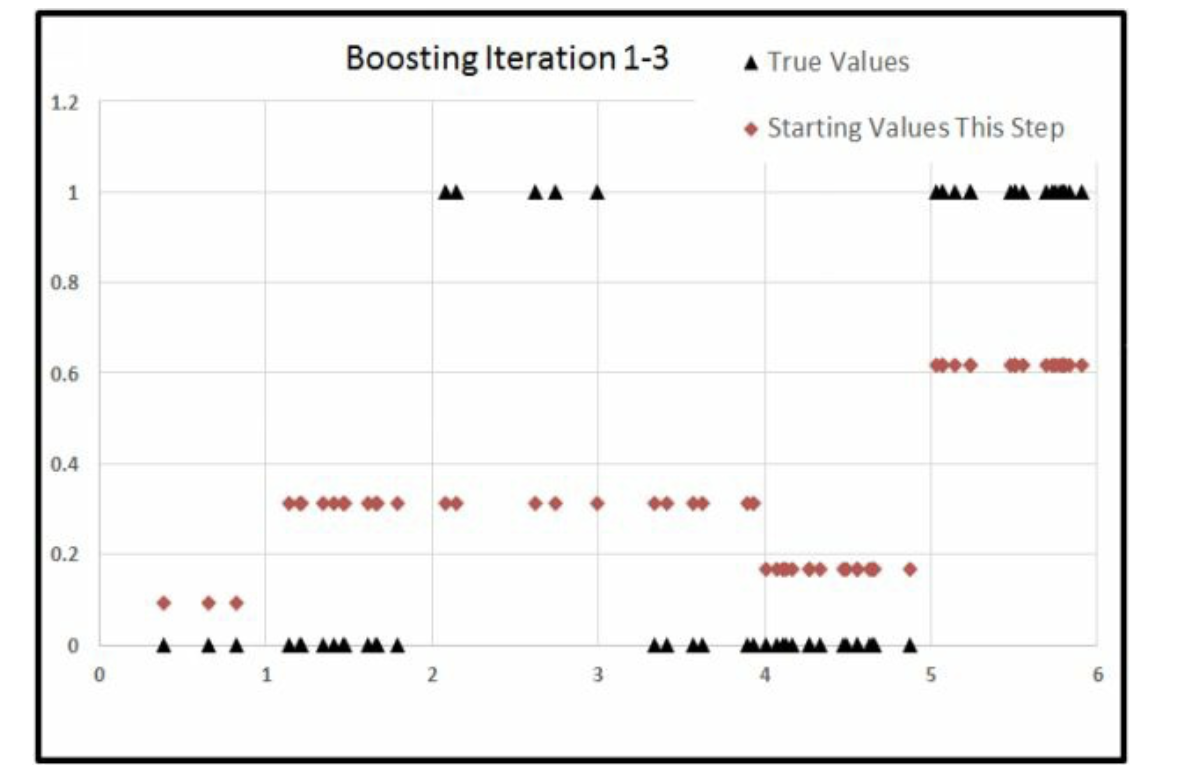
后面就不说了，以此类推。

这样就完成了Iter1。

然后开始Iter2。

10 参数总结

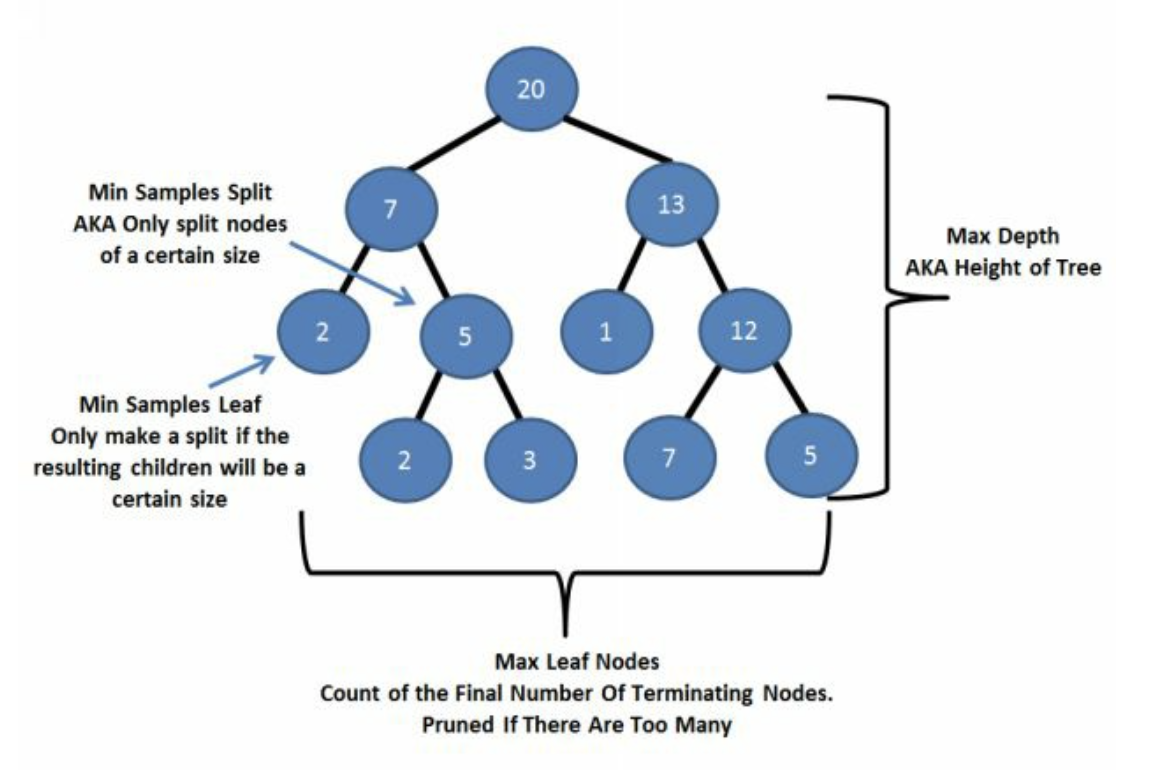
10.1 决策树参数(Python)

10.2 Boosting参数(Python)

learning_rate
n_estimators
subsample

10.3 其他参数

random_state
warm_start

11 boosting的局限性 - 特征工程

$max (x, y)$
$x^{2} + y^{2}$
$x + y$

这些都是特征工程，好处就是减少迭代次数，省时间。

例如，之前我们的例子中， $max (x, y)$ 就是要比x和y单独去跑节省时间。

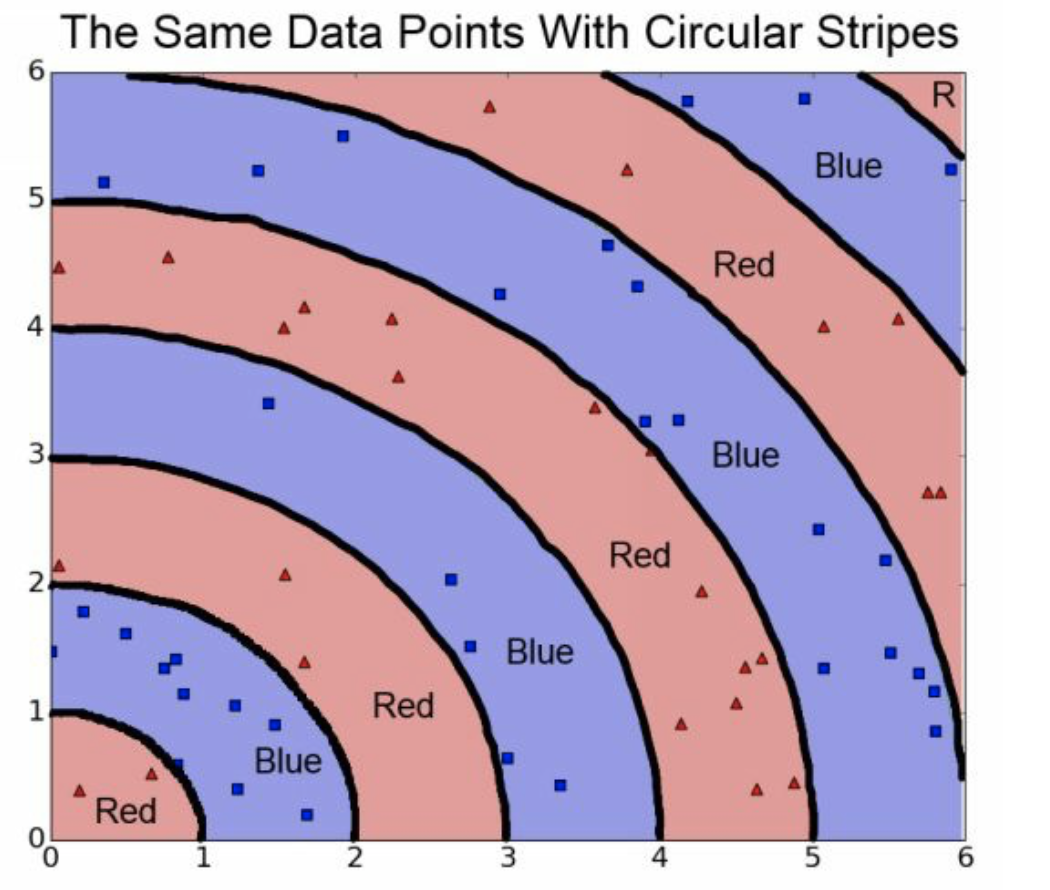
如果总体是个圆。

直接搞就很糟糕。

终于搞完了！

12 连续变量是否需要离散化

当简单对连续变量进行离散化处理时，DMLC (2016) 给出关于 Age和因变量的卡方检验证明，离散化处理不会得到的卡方值低，提高较小的信息值。

DMLC. 2016. “Understand Your Dataset with Xgboost.” 2016. http://xgboost.readthedocs.io/en/latest/R-package/discoverYourData.html.

看到我们的切分点变了，这个是根据信息增益来决定的。↩
类似于现在的标准是， X,Y $\to$ max(X,Y)的转化率是100% 我们只要把max(X,Y) $\to$ Red/Blue这一步转化做好就行了。不需要X,Y $\to$ Red/Blue↩
我们注意为什么 $z$ 的定义域那么广，为了迭代，可以一直加加减减。↩
这样的话就利用了第一次决策树的结果。下文会显示这样的利用是有效的。↩

Machine Learning With Boosting Scott Hartshorn 阅读笔记