学习内容概览
本节课程主要介绍了两种重要的生成学习算法:
- 高斯判别分析(Gaussian Discriminant Analysis, GDA)
- 朴素贝叶斯(Naive Bayes, NB)
- 拉普拉斯平滑(Laplace Smoothing)技术
这些算法虽然概念相对直观,但在实际应用中具有重要价值。
生成学习算法概述
判别式算法回顾
之前讨论的算法(如广义线性模型、牛顿算法)都属于判别式算法(discriminant algorithm),它们直接学习条件概率\(P(Y|X)\)或输出决策函数\(h_{\theta}(x) \in \{0,1\}\)。
生成式算法定义
生成学习算法(generative learning algorithm)采用不同的思路: - 学习联合概率分布\(P(x|y)\)和先验概率\(P(y)\) - 根据特征情况建模数据生成过程 - 使用贝叶斯定理进行预测
贝叶斯公式:
\[P(y=1|x) = \frac{P(x|y=1)P(y=1)}{P(x)}\]
其中边缘概率\(P(x)\)为:
\[P(x) = P(x|y=0)P(y=0) + P(x|y=1)P(y=1)\]
高斯判别分析(GDA)
多元高斯分布基础
GDA假设每个类别的特征向量服从多元高斯分布:
\[z \sim \mathcal N(\vec \mu,\Sigma) \]
其中\(\Sigma\)是协方差矩阵,\(\mu\)是均值向量。
多元高斯分布的概率密度函数:
\[p(x;\mu,\Sigma)= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\]
虽然公式看起来复杂,但在实际计算中通常不需要直接计算概率密度值。
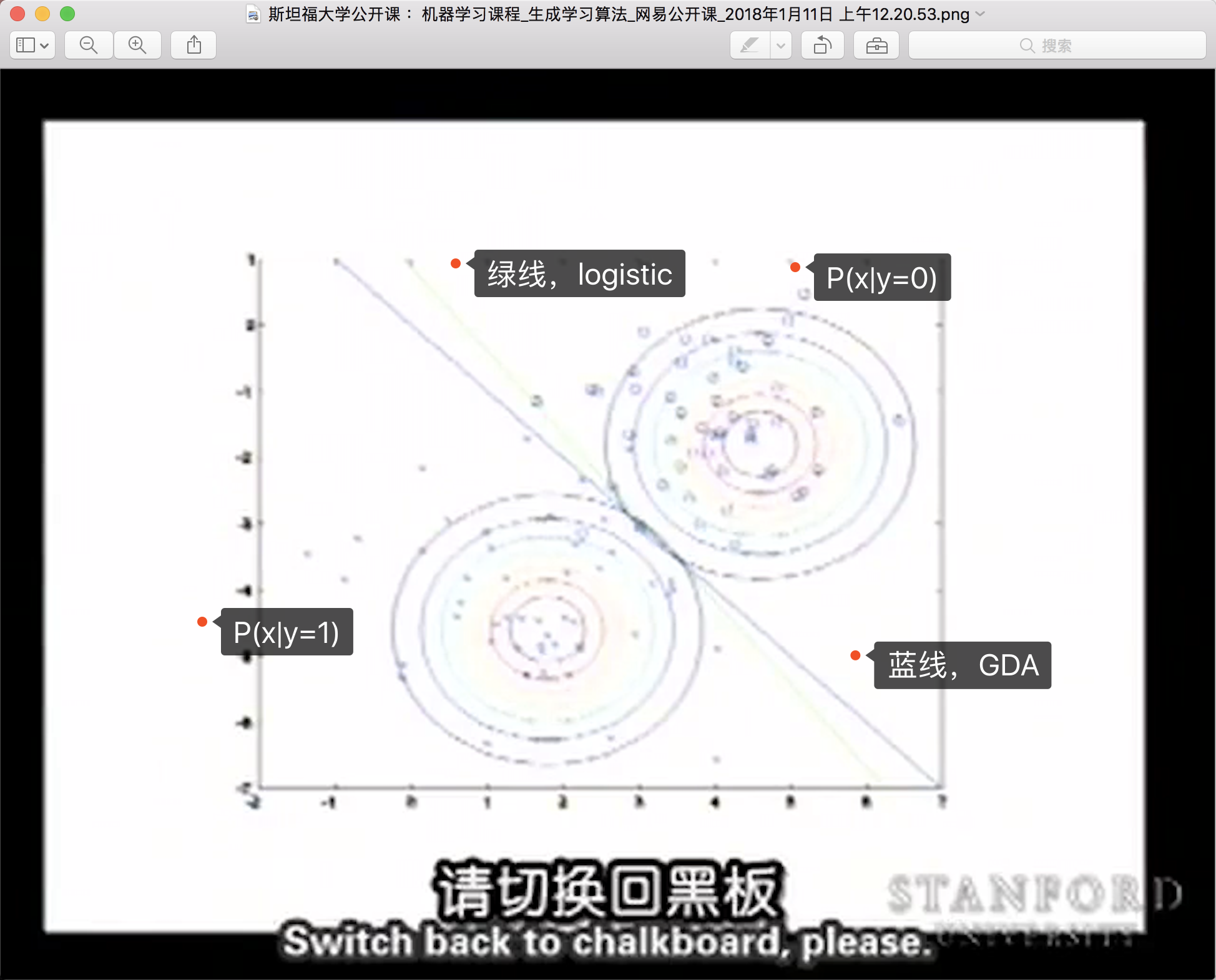
算法原理:通过计算\(P(x|y=1)\)和\(P(x|y=0)\)两个高斯分布的投影,找到它们的交点连线作为决策边界。
GDA模型定义
先验概率:
\[P(y) = \phi^y(1-\phi)^{1-y}\]
条件概率分布:
\[P(x|y=0)= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0))\]
\[P(x|y=1)= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1))\]
与逻辑回归的区别
优化目标差异:
- GDA:最大化联合概率\(\max \prod P(x^{(i)},y^{(i)})\)
- 逻辑回归:最大化条件概率\(\max \prod P(y^{(i)}|x^{(i)})\)
这是两种不同的建模思路,各有优劣,没有绝对的优劣之分。
GDA与逻辑回归的关系
理论关系
当假设特征向量\(x|y\)服从高斯分布时,通过贝叶斯定理推导出的后验概率\(P(y=1|x)\)恰好是一个逻辑函数。这意味着GDA在特定假设下等价于逻辑回归,但GDA的假设条件更严格。
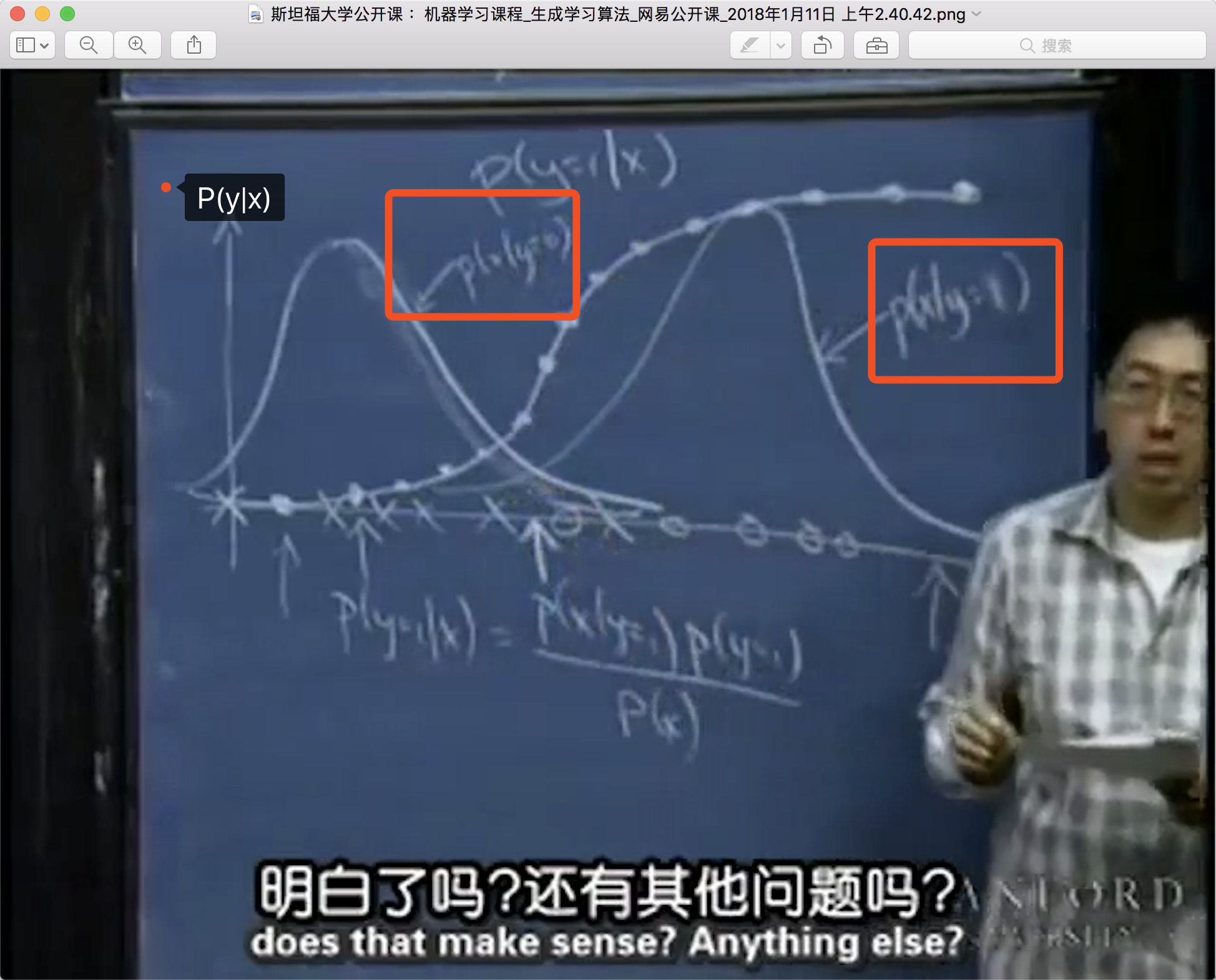
计算过程
GDA的预测过程:
- 计算\(P(x|y=1)\)和\(P(y=1)\)
- 计算边缘概率\(P(x) = P(x|y=1)P(y=1) + P(x|y=0)P(y=0)\)
- 应用贝叶斯公式得到\(P(y|x)\)
这种基于生成模型的方法提供了对数据分布的完整建模。
更一般的结论
重要定理:如果\(x|y\)服从某些特定的指数族分布,那么\(P(y=1|x)\)将是一个逻辑函数。
具体例子: - 高斯分布:\(x|y \sim \mathcal N(\mu_y,\Sigma) \to P(y=1|x)\)是逻辑函数 - 泊松分布:\(x|y=1 \sim \mathcal Poisson(\lambda_1)\)和\(x|y=0 \sim \mathcal Poisson(\lambda_0) \to P(y=1|x)\)也是逻辑函数
注意:这个关系是单向的,不能反向推导。
算法特点
GDA的优势: - 假设条件强,需要的数据量较少 - 对数据分布有完整的建模 - 在小样本情况下可能表现更好
局限性:
- 假设条件可能过于严格
- 对分布假设的敏感性较高
朴素贝叶斯(Naive Bayes)
算法动机
朴素贝叶斯是另一种生成学习算法,与GDA的主要区别在于: - GDA要求特征\(x\)是连续变量 - NB可以处理离散特征
应用场景:垃圾邮件分类
以垃圾邮件分类为例:
- \(y=1\)表示垃圾邮件
- 使用字典将邮件转换为特征向量
- 如果邮件包含字典中第\(i\)个词,则\(x_i=1\),否则\(x_i=0\)
- 特征空间:\(x \in \{0,1\}^n\),共有\(2^n\)种可能组合
参数估计问题
如果直接建模联合分布,需要估计\(2^n-1\)个参数,这在实践中是不可行的。
朴素贝叶斯假设
引入强假设:特征在给定类别下条件独立
\[\begin{alignat}{2} P(x_1,\cdots,x_n|y) & = P(x_1|y)P(x_2|y,x_1)\cdots P(x_n|y,x_1,\cdots,x_{n-1}) \\ & = P(x_1|y)P(x_2|y) \cdots P(x_n|y)\\ \end{alignat}\]
条件独立意味着\(P(x_2|y,x_1) = P(x_2|y)\),即\(x_1\)不影响\(x_2\)的分布。
虽然这个假设在现实中通常不成立,但在实践中效果很好。
参数定义与估计
条件概率参数:
\[\begin{alignat}{2} \phi_{i|y=1} &= p(x_i=1|y=1) \\ &=\frac{\sum_{i=1}^m\mathcal I\{x_j^{(i)}=1,y^{(i)}=1\}}{\sum_{i=1}^m\mathcal I\{y^{(i)}=1\}}\\ \end{alignat}\]
\[\phi_{i|y=0} = p(x_i=1|y=0)\]
先验概率:
\[\begin{alignat}{2} \phi_y &= p(y=1) \\ &=\frac{\sum_{i=1}^m\mathcal I\{y^{(i)}=1\}}{m} \\ \end{alignat}\]
预测公式:
\[p(y|x) \propto p(x|y)p(y)\]
朴素贝叶斯的假设主要体现在联合分布上,通过条件独立性简化了模型复杂度。
拉普拉斯平滑(Laplace Smoothing)
零概率问题
朴素贝叶斯的预测公式:
\[p(y=1|x) = \frac{p(x|y=1)p(y=1)}{p(x|y=1)p(y=1)+p(x|y=0)p(y=0)}\]
问题:如果训练数据中从未出现过某个特征组合\(x\),则\(p(x|y)=0\),导致:
\[p(y=1|x) = \frac{0 \cdot p(y=1)}{0}\]
出现未定义的情况。
拉普拉斯平滑技术
二分类情况:
\[P(y=1) = \frac{n_1+1}{n_1+1+n_0+1}\]
这样即使训练集中\(n_1=0\),仍然保留了一定的概率预测\(y=1\)。
多分类一般形式:
\[P(y=j)=\frac{\sum_{i=1}^m \mathcal I\{y^{(i)}=j\}+1}{m+k}\]
其中\(k\)是类别数量。
条件概率的平滑
对于条件概率参数:
\[\begin{alignat}{2} \phi_{i|y=1} &= p(x_i=1|y=1) \\ &=\frac{\sum_{i=1}^m\mathcal I\{x_j^{(i)}=1,y^{(i)}=1\}+1}{\sum_{i=1}^m\mathcal I\{y^{(i)}=1\}+2}\\ \end{alignat}\]
拉普拉斯平滑通过添加伪计数避免了零概率问题,提高了模型的鲁棒性。