• t-SNE for 2-dimensional maps | Python

t-SNE = “t-distributed stochastic neighbor embedding” 这是t-SNE的全称，主要用于高维数据可视化。高维数据，表示一个用户数据，可以用10个、100个维度去描述，也就是特征多，这个时候，为了跟业务部门展示数据的分类， t-SNE就发挥了这样的作用。

这个图可以感受一下，

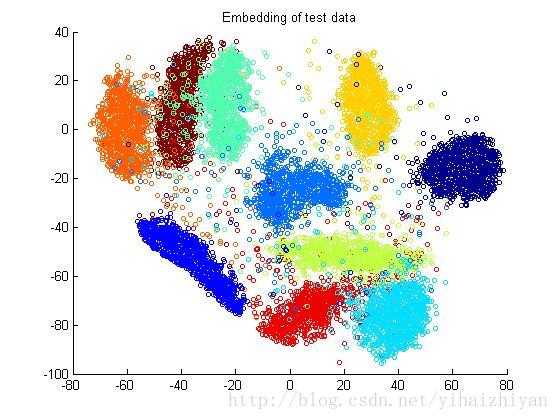
Python中， from sklearn.manifold import TSNE引入。 .fit_transform, simultaneously fits the model and transforms the data, Can’t extend the map to include new data samples. learning_rate=100, try values between 50 and 200

徐志强: t-sne是流行学习的一种，属于非线性降维的一种，主要是保证高维空间中相似的数据点在低维空间中尽量挨得近。是从sne演化而来，sne中用高斯分布衡量高维和地位空间数据点之间的相似性，t-sne主要是为了解决sne中的“拥挤问题”，用t分布定义低维空间低维空间中点的相似性。但是t-sne不能算是一种通用的降维方法吧，时间复杂度也挺高的。

• t-SNE visualization of grain dataset | Python

from sklearn.manifold import TSNE引入。¹

# Import TSNE
from sklearn.manifold import TSNE

# Create a TSNE instance: model
model = TSNE(learning_rate = 200)

# Apply fit_transform to samples: tsne_features
tsne_features = model.fit_transform(samples)

# Select the 0th feature: xs
xs = tsne_features[:,0]

# Select the 1st feature: ys
ys = tsne_features[:,1]

# Scatter plot, coloring by variety_numbers
plt.scatter(xs, ys, c = variety_numbers)
plt.show()

其中tsne_features是产生的一个\(N \times 2\)向量。

In [4]: tsne_features.shape
Out[4]: (210, 2)

• A t-SNE map of the stock market | Python

# Import TSNE
from sklearn.manifold import TSNE 

# Create a TSNE instance: model
model = TSNE(learning_rate = 50)

# Apply fit_transform to normalized_movements: tsne_features
tsne_features = model.fit_transform(normalized_movements)

# Select the 0th feature: xs
xs = tsne_features[:,0]

# Select the 1th feature: ys
ys = tsne_features[:,1]

# Scatter plot
plt.scatter(xs, ys, alpha=0.5)

# Annotate the points
for x, y, company in zip(xs, ys, companies):
    plt.annotate(company, (x, y), fontsize=5, alpha=0.75)
plt.show()

相似的变量靠的近。

我想，肯定最后能看哪个影响比较大，只是暂时我代码不知道怎么写。 而且我看了下知乎，这个东西似乎大家只是用来做聚类，就是做分类的。 今天我刚刚看到，要是这个能看影响排序，就真的厉害了！！！