1 为什么要做归一化？

tbl1 <- tibble(
  person = 1:4,
  age_yr = c(35,40,35,40),
  height_cm = c(190,190,160,160)
)
tbl1

## # A tibble: 4 x 3
##   person age_yr height_cm
##    <int>  <dbl>     <dbl>
## 1      1     35       190
## 2      2     40       190
## 3      3     35       160
## 4      4     40       160

tbl1 %>%
  ggplot(aes(x = age_yr, y = height_cm, col = as.factor(person))) +
    geom_point() +
    xlim(0,60) +
    ylim(150,200)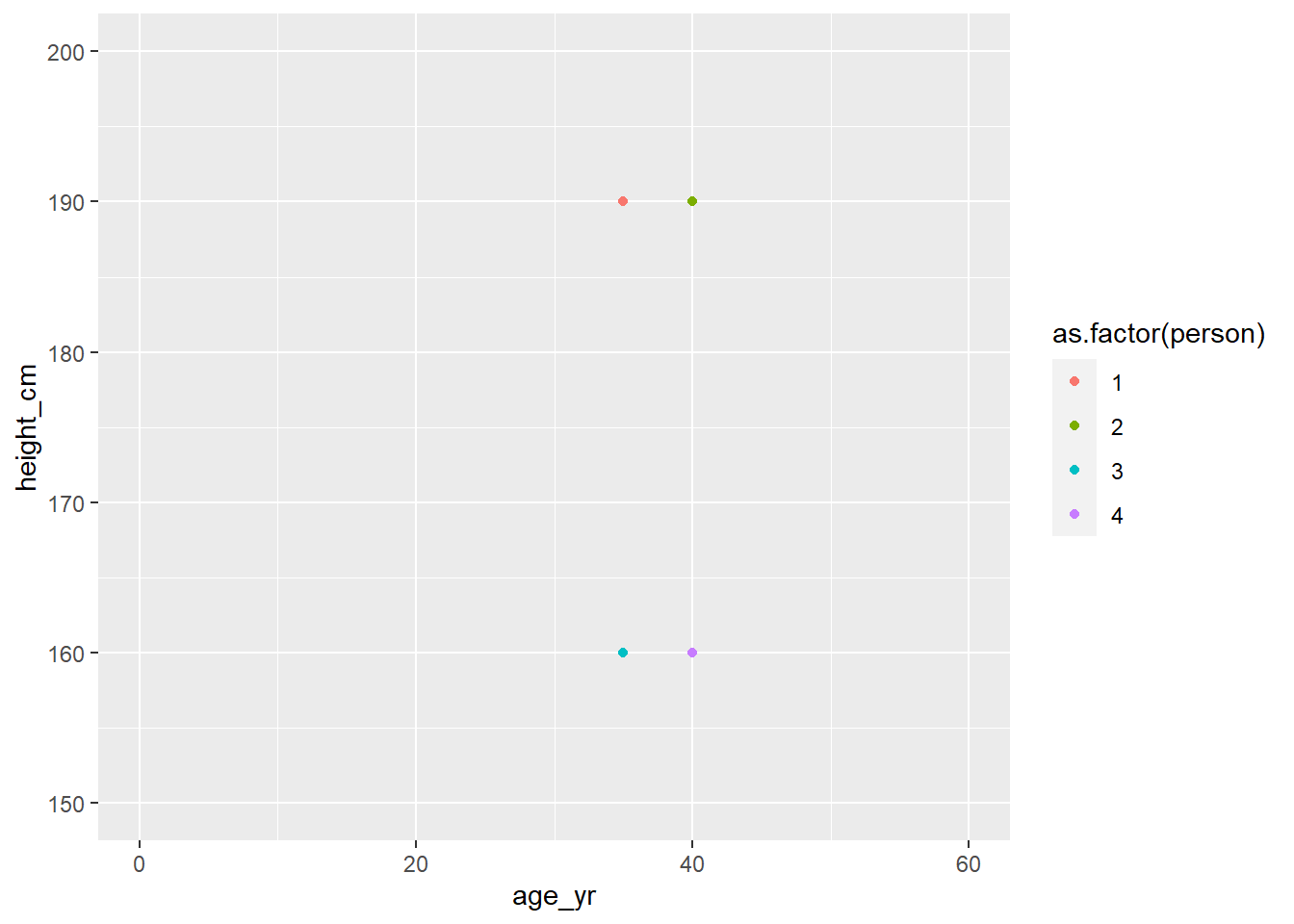

看这张图我们会发现1和2比较相似，3和4比较相似。

但是当我们把身高单位变换后，

tbl2 <- tbl1 %>%
  mutate(height_ft = height_cm / 30.48)
tbl2 %>%
  ggplot(aes(x = age_yr, y = height_ft, col = as.factor(person))) +
    geom_point() +
    xlim(35,40) +
    ylim(4,7)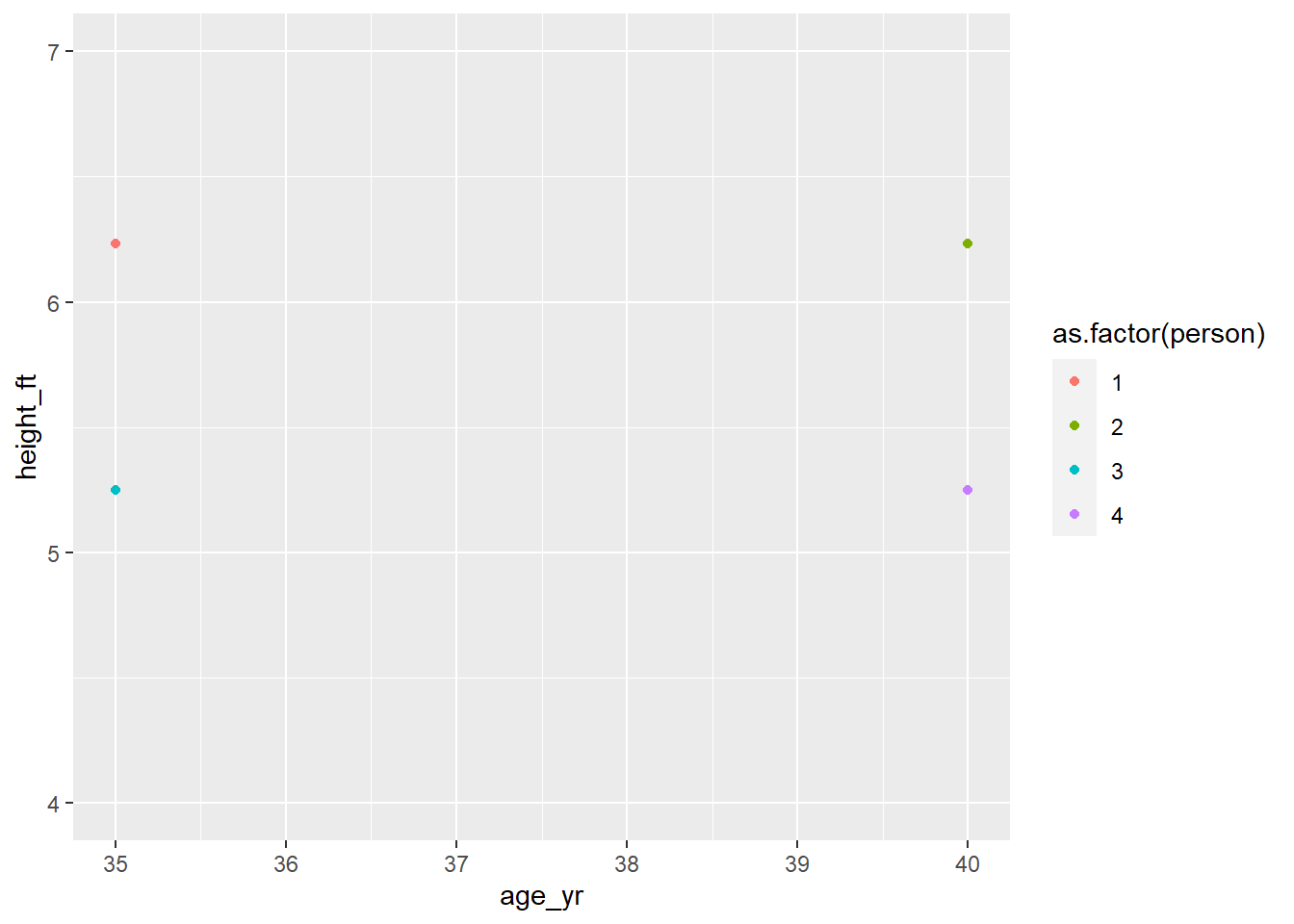

我们会发现1和3比较相似，2和4比较相似，因此我们需要对数据进行标准化。

tbl1 %>%
  mutate(age_yr_scaled = scale(age_yr), height_cm = scale(height_cm))

## # A tibble: 4 x 4
##   person age_yr height_cm[,1] age_yr_scaled[,1]
##    <int>  <dbl>         <dbl>             <dbl>
## 1      1     35         0.866            -0.866
## 2      2     40         0.866             0.866
## 3      3     35        -0.866            -0.866
## 4      4     40        -0.866             0.866

我们会发现他们四个都很相似。

例子参考 Kalisch (2012) 和 Yu (2015)， 但是当数据单位一致时，从实际出发，没必要标准化 (Kalisch 2012; Yu 2015)，比如宏观数据，都是统一的货币单位时。

2 梯度下降的方式理解

忆臻 (2017) 给出了到位的解释，感觉蛮到位。

就是说，我们假设一个二元回归，

\[y = \beta_1 x_1 + \beta_2 x_2 + u\]

损失函数，

\[J = min \sum{(y - \hat \beta_1 x_1 + \hat \beta_2 x_2)^2}\]

做了归一化的\(\hat \beta_1\)和\(\hat \beta_2\)接近，因此在以\(\hat \beta_1\)和\(\hat \beta_2\)为坐标系的直线坐标系中，图像更接近于圆。

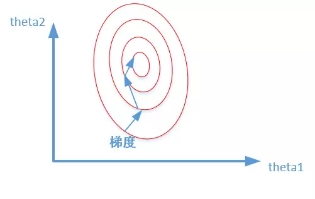
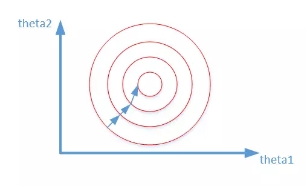
因此梯度下降的走位就不会那么风骚了。

3 max min 标准化

归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为标量。在多种计算中都经常用到这种方法。

举个例子，将\(X = \{x_1,x_2,...,x_n\}\)转化为\(\{\tilde x_1,\tilde x_2,...,\tilde x_n\}\)，公式变化为（一种情况）

\[\tilde x_i = \frac{x-min(x)}{max(X)-min}\]

4 z标准化在python中

可以在python中自行构建代码 (Aruliah 2017)。

\[\tilde x_i = \frac{x-\bar x}{\sigma (X)}\]

Python的函数

def zscore(series): 
      return (series - series.mean()) / series.std()

这里的series是未知数，可以写成l、x等等。

5 StandardScalar在python中

StandardScalar就是标准化，所谓的标准化就是\(\mu = 0\)和\(\sigma = 1\)。

\[\tilde x = \frac{x-\bar x}{\sigma_x}\]

\[E(\tilde x) = E(\frac{x-\bar x}{\sigma_x}) = E(\frac{x}{\sigma_x})-E(\frac{\bar x}{\sigma_x})=0\]

\[Var(\tilde x) = Var(\frac{x-\bar x}{\sigma_x}) = \frac{1}{\sigma_{x}^2} \cdot Var(x-\bar x) = \frac{Var(x)}{\sigma_{x}^2} = 1\]

from sklearn.preprocessing import StandardScalar引入。

6 聚类需要使用归一化

比如点\(x(0.1,10000)\)和\(y(0.9,9999)\)表示样本内的两个点，其中有两个特征， 第一个特征的\(range = [0.1,0.9]\)， 第二个特征的\(range = [9999,10000]\)， 显然不归一化的话，第一个特征完全被弱化了。 (张腾 2017)

7 标准化与归一化的区别

简单来说，标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”¹。规则为l2的归一化公式如下：

\[\tilde x = \frac{x}{|x|}\]

\[|x|^2 = \sum_{i=1}^mx_i\]

其中\(x\)表示一个行向量，即一个用户的数据。 \(m\)表示有m个特征。